题目内容
【题目】如图,直角梯形ABCD与等边△ABE所在的平面互相垂直,AB∥CD,AB⊥BC,AB=2CD=AD=2,F为线段EA上的点,且EA=3EF. 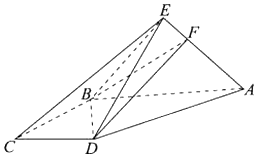
(I)求证:EC∥平面FBD
(Ⅱ)求多面体EFBCD的体积.
【答案】解:(Ⅰ)连接AC、BD交于点O,连接FO,
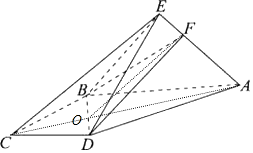
在梯形ABCD中,有△DOC与△BOA相似,可得OA=2OC,AC=3OC,
又EA=3EF,∴FO∥EC
又FO面FBD,EC面FBD
平面ACE∩平面FBD=FM.
∴EC∥平面FBD;
(Ⅱ)多面体EFBCD的体积V=VE﹣ABCD﹣VF﹣ABD
= ![]() ×
× ![]() =
= ![]() .
.
【解析】(Ⅰ)连接AC、BD交于点O,连接FO,可得AC=3OC,又EA=3EF,得FO∥EC即可证得EC∥平面FBD (Ⅱ)多面体EFBCD的体积V=VE﹣ABCD﹣VF﹣ABD= ![]() ×
× ![]() =
= ![]()
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.

练习册系列答案
相关题目