题目内容
【题目】经过坐标原点
的两条直线与椭圆
：
分别相交于点
、
和点
、
，其中直线
经过的左焦点
，直线
经过的右焦点
.当直线不垂直于坐标轴时，与
的斜率乘积为
.
（1）求椭圆的方程；
（2）求四边形
面积的最大值.
【答案】（1）
（2）最大值6.
【解析】
（1）设
，
，由对称性可知
，由
，
，相减得
，而直线
与直线
的斜率乘积为
，所以
，由题意可知
，利用
，这样可求出
的值，进而求出椭圆的标准方程；
（2）由题设
不平行于
轴，设：
，与
联立得
，由对称性四边形
是平行四边形，其面积
的等于
面积的4倍，于是
，利用根与系数的关系，和换元法以及求导法，可以求出四边形面积的最大值.
解：（1）设，，由对称性，直线与直线的斜率乘积为.
由，，相减得.
所以，因为
，所以
，
，
的方程为.
（2）由题设不平行于轴，设：，与联立得.
，
.
由对称性四边形是平行四边形，其面积的等于面积的4倍，于是 
.
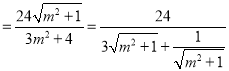设
，当
时，
，函数
单调递增，
所以当
，即
时，取最大值6.
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
【题目】某公司为了预测下月产品销售情况，找出了近7个月的产品销售量
（单位：万件）的统计表：
月份代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售量 |
|
|
|
|
|
|
|
但其中数据污损不清，经查证
，
，
.
（1）请用相关系数说明销售量与月份代码
有很强的线性相关关系；
（2）求关于
的回归方程（系数精确到0.01）；
（3）公司经营期间的广告宣传费
（单位：万元）（
），每件产品的销售价为10元，预测第8个月的毛利润能否突破15万元，请说明理由.（毛利润等于销售金额减去广告宣传费）
参考公式及数据：
，相关系数
，当
时认为两个变量有很强的线性相关关系，回归方程
中斜率和截距的最小二乘估计公式分别为
，
.
