题目内容
【题目】已知函数
，
.
（Ⅰ）当
时，求
的最小值；
（Ⅱ）若有两个零点，求参数
的取值范围
【答案】（Ⅰ）0；
（Ⅱ）
.
【解析】
（Ⅰ）求函数的定义域，再求导，判别导函数的正负可得原函数的单调性，可求得最小值；
（Ⅱ）对a进行分类讨论，分别利用其导函数的应用，判别其单调性，求其最值，可得参数a的范围.
（Ⅰ）
,定义域
当
时, 
,由于
在恒成立
故
在
单调递减, 在
单调递增.
故 
（Ⅱ）
当时, 在单调递减, 在单调递增,只有一个零点
当
时,
,故
在恒成立,
故在单调递减, 在单调递增,
故当时, 没有零点.
当时,令 
,得
,
在单调递减, 在单调递增. 
,
在有两个零点，
在
单调递减,在
单调递增,在
单调递减,在
单调递增，
,又
此时有两个零点，
综上有两个零点,则
练习册系列答案
相关题目
【题目】某种商品价格与该商品日需求量之间的几组对照数据如下表，经过进一步统计分析，发现y与x具有线性相关关系．
价格x（元/kg） | 10 | 15 | 20 | 25 | 30 |
日需求量y（kg） | 11 | 10 | 8 | 6 | 5 |
（1）根据上表给出的数据，求出y与x的线性回归方程
；
（2）利用（1）中的回归方程，当价格
元/kg时，日需求量y的预测值为多少？
（参考公式：线性回归方程，其中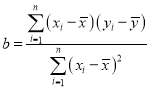
，
．）
