题目内容
等边三角形ABC与正方形ABDE有一公共边AB,二面角C-AB-D的余弦值为
| ||
| 3 |
分析:先找出二面角的平面角,建立边之间的等量关系,再利用向量法将所求异面直线用基地表示,然后利用向量的所成角公式求出所成角即可.
解答: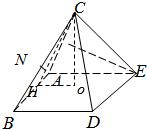 解:设AB=2,作CO⊥面ABDE,
解:设AB=2,作CO⊥面ABDE,
OH⊥AB,则CH⊥AB,∠CHO为二面角C-AB-D的平面角CH=
,OH=CH•cos∠CHO=1,
结合等边三角形ABC与正方形ABDE可知此四棱锥为正四棱锥,
则AN=EM=CH=
=
(
+
),
=
-
,
•
=
(
+
)•(
-
)=
故EM,AN所成角的余弦值
=
故答案为:
 解:设AB=2,作CO⊥面ABDE,
解:设AB=2,作CO⊥面ABDE,OH⊥AB,则CH⊥AB,∠CHO为二面角C-AB-D的平面角CH=
| 3 |
结合等边三角形ABC与正方形ABDE可知此四棱锥为正四棱锥,
则AN=EM=CH=
| 3 |
| AN |
| 1 |
| 2 |
| AC |
| AB |
| EM |
| 1 |
| 2 |
| AC |
| AE |
| AN |
| EM |
| 1 |
| 2 |
| AB |
. |
| AC |
| 1 |
| 2 |
| AC |
| AE |
| 1 |
| 2 |
故EM,AN所成角的余弦值
| ||||
|
|
| 1 |
| 6 |
| 1 |
| 6 |
点评:本小题主要考查异面直线所成的角,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
相关题目
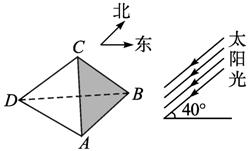
 、
、 ,直线a、b,若
,直线a、b,若 ,
, ,则
,则 ;
;