题目内容
11、下列命题中正确命题的个数是( )
①经过空间一点一定可作一平面与两异面直线都平行;
②已知平面α、β,直线a、b,若α∩β=a,b⊥a,则b⊥α;
③有两个侧面垂直于底面的四棱柱为直四棱柱;
④四个侧面两两全等的四棱柱为直四棱柱;
⑤底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥;
⑥底面是等边三角形,∠APB=∠BPC=∠CPA,则三棱锥P-ABC是正三棱锥.
①经过空间一点一定可作一平面与两异面直线都平行;
②已知平面α、β,直线a、b,若α∩β=a,b⊥a,则b⊥α;
③有两个侧面垂直于底面的四棱柱为直四棱柱;
④四个侧面两两全等的四棱柱为直四棱柱;
⑤底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥;
⑥底面是等边三角形,∠APB=∠BPC=∠CPA,则三棱锥P-ABC是正三棱锥.
分析:①若该点在某一条直线上,则直线在所作的平面内.
②根据面面垂直的判定定理判断.
③根据直棱柱的条件判断,看侧棱与底面是否垂直.
④根据直棱柱的条件判断,看侧棱与底面是否垂直.
⑤根据正三棱锥的定义判断.
⑥根据正三棱锥的定义判断.
②根据面面垂直的判定定理判断.
③根据直棱柱的条件判断,看侧棱与底面是否垂直.
④根据直棱柱的条件判断,看侧棱与底面是否垂直.
⑤根据正三棱锥的定义判断.
⑥根据正三棱锥的定义判断.
解答:解:①若该点在某一条直线上,则不正确.
②根据面面垂直的判定,直线b不一定在平面β内,所以不正确.
③如果这个两个侧面互相平行,则不一定有侧棱垂直于底面,所以不正确.
④四个侧面两两全等不能保证侧棱与底面垂直.
⑤侧面都是等腰三角形若不是腰共顶点,则不正确.
⑥底面是等边三角形,∠APB=∠BPC=∠CPA,不能保证顶点在底面的身影为中心,则不正确.
故选A
②根据面面垂直的判定,直线b不一定在平面β内,所以不正确.
③如果这个两个侧面互相平行,则不一定有侧棱垂直于底面,所以不正确.
④四个侧面两两全等不能保证侧棱与底面垂直.
⑤侧面都是等腰三角形若不是腰共顶点,则不正确.
⑥底面是等边三角形,∠APB=∠BPC=∠CPA,不能保证顶点在底面的身影为中心,则不正确.
故选A
点评:本题主要考查棱锥的结构特征及棱锥的分类,考查地很全面,要求掌握要熟练,属中档题.

练习册系列答案
相关题目
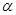 内,A、B、C三点都在平面
内,A、B、C三点都在平面 ,使
,使 ;②若
;②若 是第一象限角,且
是第一象限角,且 ,则
,则 ;
; 是偶函数; ④函数
是偶函数; ④函数 的图象向左平移
的图象向左平移 个单位,得到函
个单位,得到函 的图象.
的图象.