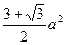题目内容
如图在正三棱锥P-ABC中,侧棱长为3,底面边长为2,E为BC的中点,
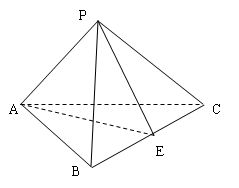
(1)求证:BC⊥PA
(2)求点C到平面PAB的距离
【答案】
(1)详见解析;(2)
【解析】
试题分析:(1)解题思路证线面垂直得线线垂直,详见解析。(2)过点P做面ABC的垂线,垂足为O,因为三棱锥P-ABC为正三棱锥,则点O为底面三角形的中心。则 ,在直角三角形POA中求PO,PO即为三棱锥P-ABC的高,可求得三棱锥体积为
,在直角三角形POA中求PO,PO即为三棱锥P-ABC的高,可求得三棱锥体积为 。又因为三角形PAB各边长已知可求其面积,设出点C到面PAB的距离h,也可表示出三棱锥的体积
。又因为三角形PAB各边长已知可求其面积,设出点C到面PAB的距离h,也可表示出三棱锥的体积 ,根据体积相等即
,根据体积相等即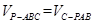 ,可求出h。
,可求出h。

试题解析:证明(1)E为BC的中点,又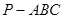 为正三棱锥
为正三棱锥

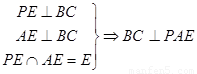 因为
因为 ,所以BC⊥PA
,所以BC⊥PA
(2)设点C到平面PAB的距离为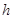 。
。
则

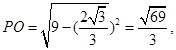 10分
10分
 12分
12分
考点:线线垂直,点到面的距离

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目




 B.
B. C.
C. D.
D.