题目内容
在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥平面ABCD,AB=PD=a.点E为侧棱PC的中点,又作DF⊥PB交PB于点F.则PB与平面EFD所成角为( )
| A.30° | B.45° | C.60° | D.90° |
D
建立空间直角坐标系D—xyz,D为坐标原点.P(0,0,a),B(a,a,0),
 =(a,a,-a),又
=(a,a,-a),又 =
= ,
,
 =0+
=0+ -
- =0,
=0,
所以PB⊥DE.由已知DF⊥PB,又DF∩DE=D,
所以PB⊥平面EFD,所以PB与平面EFD所成角为90°,选D.
 =(a,a,-a),又
=(a,a,-a),又 =
= ,
, =0+
=0+ -
- =0,
=0,所以PB⊥DE.由已知DF⊥PB,又DF∩DE=D,
所以PB⊥平面EFD,所以PB与平面EFD所成角为90°,选D.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 ,点E在侧棱AA1上,点F在侧棱BB1上,且AE=2
,点E在侧棱AA1上,点F在侧棱BB1上,且AE=2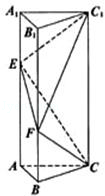
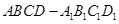
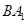 异面
异面
 ABCD中,EA=EB,AB∥CD,AB⊥BC,AB=2CD.
ABCD中,EA=EB,AB∥CD,AB⊥BC,AB=2CD.
 ;若不存在,说明理由.
;若不存在,说明理由.
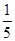


 分别是正方体
分别是正方体 的棱
的棱 的中点,点
的中点,点 分别是线段
分别是线段 与
与 上的点,则与平面
上的点,则与平面 垂直的直线
垂直的直线 有( )
有( )
 中,E,F,M分别是AB、AD、
中,E,F,M分别是AB、AD、 的中点,又P、Q分别在线段
的中点,又P、Q分别在线段 上,且
上,且 ,设面
,设面 面MPQ=
面MPQ= ,则下列结论中不成立的是( )
,则下列结论中不成立的是( )
 面ABCD
面ABCD AC
AC 外一点可以作无数条直线与平面
外一点可以作无数条直线与平面 垂直平面
垂直平面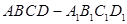 中,线段
中,线段 上(不包括端点)各有一点
上(不包括端点)各有一点 ,且
,且 ,下列说法中,不正确的是( )
,下列说法中,不正确的是( ) 四点共面
四点共面 与平面
与平面 所成的角为定值
所成的角为定值
 的大小为
的大小为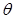 ,则
,则 的最小值为
的最小值为