题目内容

15．函数y=-x2+3x-1的单调性是在区间[$\frac{3}{2}$，+∞）上是减函数．

分析 根据函数y是二次函数，结合二次函数的图象与性质，即可求出函数y的单调减区间．

解答 解：∵函数y=-x2+3x-1是二次函数，且开口向下，对称轴是x=$\frac{3}{2}$；
∴在对称轴的右侧，函数y=-x2+3x-1是单调减函数；
∴函数y=-x2+3x-1的单调减区间是[$\frac{3}{2}$，+∞）．
故答案为：[$\frac{3}{2}$，+∞）．

点评 本题考查了二次函数的图象与性质的应用问题，是基础题目．

练习册系列答案
相关题目
5．下列结论中，正确的是（　　）
A．2014cm长的有向线段不可能表示单位向量
B．若0是直线l上的一点，单位长度已选定，则l上有且只有两个点A，B，使得$\overrightarrow{OA}$，$\overrightarrow{OB}$是单位向量
C．方向为北偏西50°的向量与南偏东50°的向量不可能是平行向量
D．一人从A点向东走500米到达B点，则$\overrightarrow{AB}$不能表示这个人从A点到B点的位移
6．（1）已知函数f（x）=$\frac{1}{2}$x-$\frac{1}{4}$sinx-$\frac{\sqrt{3}}{4}$cosx的图象在点A（x0，f（x0））处的切线斜率为$\frac{1}{2}$，求tanx0的值．
（2）对于正整数n，设曲线y=xn（1-x）在x=2处的切线与y轴交点的纵坐标为an，求数列{$\frac{{a}_{n}}{n+1}$}的前n项和．
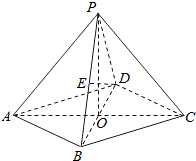3．在四棱锥P-ABCD中，底面是边长为2的菱形，∠DAB=60°，对角线AC与BD相交于点O，PO⊥平面ABCD，PB⊥平面ABCD所成的角为60°．
（1）求四棱锥P-ABCD的体积；
（2）若E是PB的中点，求异面直线DE与PA所成角的余弦值；
（3）求二面角C-PB-D的正切值．
10．已知0＜α＜$\frac{π}{2}$，0＜β＜$\frac{π}{2}$，且，$\frac{sinβ}{sinα}$=cos（α+β），α+β≠$\frac{π}{2}$，则tanβ的最大值为$\frac{\sqrt{2}}{4}$．
20．解不等式loga（x2-x-2）＜loga（2x2-7x+3）（0＜a＜1）
7．-268°是第（　　）象限的角．
A．一B．二C．三D．四
9．在f（x）=$\frac{1}{1+{x}^{a-b}+{x}^{a-c}}$+$\frac{1}{1+{x}^{b-c}+{x}^{b-a}}$+$\frac{1}{1+{x}^{c-a}+{x}^{c-b}}$中，取x≠0的一些特殊的值，均有f（x）=1，一般地，x≠0时，是否恒有f（x）=1？证明你的结论．
10．对于任意的实数k，关于x的方程x2-5x+4=k（x-a）恒有两个不相等的实数根，则实数a的取值范围为1＜a＜4．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网