题目内容
10.已知0<α<$\frac{π}{2}$,0<β<$\frac{π}{2}$,且,$\frac{sinβ}{sinα}$=cos(α+β),α+β≠$\frac{π}{2}$,则tanβ的最大值为$\frac{\sqrt{2}}{4}$.分析 首先对三角函数关系式进行恒等变换,整理成tanβ=$\frac{1}{2tanα+\frac{1}{tanα}}$,再利用基本不等式求得它的最大值,
解答 解:由$\frac{sinβ}{sinα}$=cos(α+β),可得:sinβ=sinαcos(α+β),即 sinβ=sinα(cosαcosβ-sinαsinβ)=sinαcosαcosβ-sinαsinαsinβ,
等式两边都除以cosβ得到:tanβ=sinαcosα-sin2αtanβ,
整理得:tanβ=$\frac{sinαcosα}{1+si{n}^{2}α}$=$\frac{tanα}{2ta{n}^{2}α+1}$,由于α,β∈(0,$\frac{π}{2}$),α+β≠$\frac{π}{2}$,
所以:tanβ=$\frac{1}{2tanα+\frac{1}{tanα}}$≤$\frac{1}{2\sqrt{2}}$=$\frac{\sqrt{2}}{4}$,当且仅当 tanα=$\frac{\sqrt{2}}{2}$时,取等号,故tanβ的最大值为$\frac{\sqrt{2}}{4}$.
故答案为:$\frac{\sqrt{2}}{4}$.
点评 本题考查的知识要点:三角函数关系式的恒等变换,基本不等式的应用,属于中档题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
18.已知f(x)在R上是奇函数且满足f(x+4)=f(x),若x∈(0,2)时,f(x)=2x2,则f(11)的值为( )
| A. | -2 | B. | 2 | C. | -98 | D. | 98 |
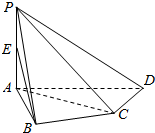 在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PA上的一点.
在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PA上的一点.