题目内容
3.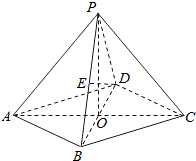 在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD相交于点O,PO⊥平面ABCD,PB⊥平面ABCD所成的角为60°.
在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD相交于点O,PO⊥平面ABCD,PB⊥平面ABCD所成的角为60°.(1)求四棱锥P-ABCD的体积;
(2)若E是PB的中点,求异面直线DE与PA所成角的余弦值;
(3)求二面角C-PB-D的正切值.
分析 (1)由PO⊥平面ABCD,得∠PBO是PB与平面ABCD所成的角,∠PBO=60°.由此我们可以计算出PO即棱锥的高,及底面菱形的面积,代入即可得到棱锥的体积.
(2)取AB的中点F,连接EF、DF.由E是PB的中点,得EF∥PA,则∠FED是异面直线DE与PA所成角(或它的补角),然后解三角形FED求出夹角.
(3)作AM⊥PB,垂足为M,连接CM,则CM⊥PB,∠AMC为二面角C-PB-D的平面角,利用余弦定理可得结论.
解答 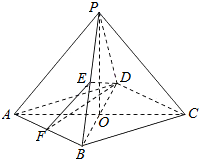 解:(1)在四棱锥P-ABCD中,由PO⊥平面ABCD,得∠PBO是PB与平面ABCD所成的角,∠PBO=60°.
解:(1)在四棱锥P-ABCD中,由PO⊥平面ABCD,得∠PBO是PB与平面ABCD所成的角,∠PBO=60°.
在Rt△AOB中BO=ABsin30°=1,由PO⊥BO,
于是,PO=BOtan60°=$\sqrt{3}$,而底面菱形的面积为2$\sqrt{3}$.
∴四棱锥P-ABCD的体积V=$\frac{1}{3}$×2$\sqrt{3}$×$\sqrt{3}$=2.
(2)取AB的中点F,连接EF、DF.
由E是PB的中点,得EF∥PA,
∴∠FED是异面直线DE与PA所成角(或它的补角),
在Rt△AOB中AO=ABcos30°=$\sqrt{3}$=OP,
于是,在等腰Rt△POA中,PA=$\sqrt{6}$,则EF=$\frac{\sqrt{6}}{2}$.
在正△ABD和正△PBD中,DE=DF=$\sqrt{3}$,
cos∠FED=$\frac{\frac{1}{2}EF}{DE}$=$\frac{\sqrt{2}}{4}$
∴异面直线DE与PA所成角的余弦值为$\frac{\sqrt{2}}{4}$;
(3)作AM⊥PB,垂足为M,连接CM,则CM⊥PB,∴∠AMC为二面角C-PB-D的平面角.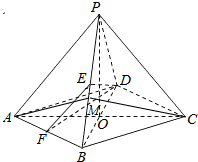
△PAB中,PA=$\sqrt{6}$,PB=2,AB=2,∴由等面积可得$\frac{1}{2}×\sqrt{6}×\sqrt{4-\frac{6}{4}}$=$\frac{1}{2}×2×AM$,
∴AM=$\frac{\sqrt{15}}{2}$,
∴cos∠AMC=$\frac{\frac{15}{4}+\frac{15}{4}-12}{2×\frac{\sqrt{15}}{2}×\frac{\sqrt{15}}{2}}$=-$\frac{3}{5}$
∴二面角C-PB-D的正切值为-$\frac{4}{3}$.
点评 本题考查四棱锥P-ABCD的体积,异面直线DE与PA所成角的余弦值,二面角C-PB-D的正切值,考查学生分析解决问题的能力,属于中档题.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案| A. | -2 | B. | 2 | C. | -98 | D. | 98 |
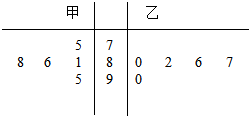 如图是甲乙两同学在高三的五次月考成绩的茎叶图,对甲乙的考试成绩作比较,请你写出两个统计结论:
如图是甲乙两同学在高三的五次月考成绩的茎叶图,对甲乙的考试成绩作比较,请你写出两个统计结论: