题目内容
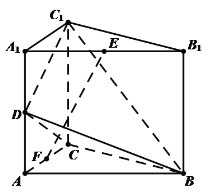
【题目】如图,在斜三梭柱ABC﹣A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,E是棱AB上一点,且OE∥平面BCC1B1
(1)求证:E是AB中点;
(2)若AC1⊥A1B,求证:AC1⊥BC.
【答案】
(1)证明:连结BC1,取AB中点E′,
∵侧面AA1C1C是菱形,AC1与A1C交于点O,
∴O为AC1的中点,
∵E′是AB的中点,
∴OE′∥BC1;
∵OE′平面BCC1B1,BC1平面BCC1B1,
∴OE′∥平面BCC1B1,
∵OE∥平面BCC1B1,
∴E,E′重合,
∴E是AB中点

(2)证明:∵侧面AA1C1C是菱形,
∴AC1⊥A1C,
∵AC1⊥A1B,A1C∩A1B=A1,A1C平面A1BC,A1B平面A1BC,
∴AC1⊥平面A1BC,
∵BC平面A1BC,
∴AC1⊥BC.
【解析】(1)利用同一法,首先通过连接对角线得到中点,进一步利用中位线,得到线线平行,进一步利用线面平行的判定定理,得到结论.(2)利用菱形的对角线互相垂直,进一步利用线面垂直的判定定理,得到线面垂直,最后转化成线线垂直.

练习册系列答案
相关题目
【题目】某工厂生产甲、乙两种产品,已知生产每吨甲、乙两种产品所需煤、电力、劳动力、获得利润及每天资源限额(最大供应量)如表所示:
资源 消耗量 产品 | 甲产品(每吨) | 乙产品(每吨) | 资源限额(每天) |
煤( | 9 | 4 | 360 |
电力( | 4 | 5 | 200 |
劳力(个) | 3 | 10 | 300 |
利润(万元) | 7 | 12 |
问:每天生产甲、乙两种产品各多少吨,获得利润总额最大?