题目内容
【题目】已知数列
和
满足：
，
，
，其中
.
（1）求数列和的通项公式；
（2）记数列的前
项和为
，问是否存在正整数
，使得
成立？若存在，求的最小值；若不存在，请说明理由.
【答案】（1）
；（2）存在正整数
，使得
成立，且的最小值为3
【解析】试题分析：（1）
（
）中n用n-1代，得 
，两式作差，可求得
，要检验n=1时。（2）
通过待定系数法可求得
，再由
，
得：
，可知{
}是等比数列，求得
。另由错位相减法可求得前n项和
,代入
，即：
化简得：
，由于f(m)=
是单调递增函数，所以采用逐个检验法可求解。
试题解析：（1）由 （）①
得：当
时，
，故
当
时， ②
①－②得：
（）
∴
又上式对也成立
∴
由变形得：
由，得：
∴
，故
（2）由（1）知：
③
④
③－④得：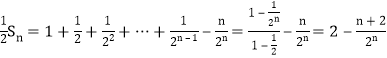
∴
假设存在正整数
，使得，即：
化简得：
由指数函数与一次函数的单调性知，
是关于的增函数
又
，
∴当
时，恒有
∴存在正整数，使得成立，且的最小值为3.
练习册系列答案
相关题目
