题目内容
【题目】已知△ABC的内角A,B,C的对边分别为a,b,c,且满足cos2B﹣cos2C﹣sin2A=sinAsinB.
(1)求角C;
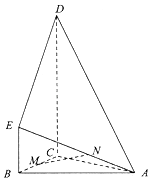
(2)若c=2 ![]() ,△ABC的中线CD=2,求△ABC面积S的值.
,△ABC的中线CD=2,求△ABC面积S的值.
【答案】
(1)解:∵△ABC的三个内角为A,B,C,且cos2B﹣cos2C﹣sin2A=sinAsinB.
sin2C﹣sinAsinB=sin2A+sin2B,
∴由正弦定理化简得:c2﹣ab=a2+b2,
∴cosC= ![]() ,
,
可得:cosC= ![]()
∵0<C<π,
∴C= ![]() .
.
(2)解:设∠ADC=α,则∠CDB=π﹣α.
在△ADC中,由余弦定理可得:b2= ![]() ﹣
﹣ ![]() ,
,
在△CDB中,由余弦定理可得:a22= ![]() ﹣2×
﹣2× ![]() cos(π﹣α),
cos(π﹣α),
∴b2+a2=20,
在△ABC中,由余弦定理可得: ![]() =b2+a2﹣2ba
=b2+a2﹣2ba ![]() ,化为:b2+a2+ba=24.
,化为:b2+a2+ba=24.
∴ba=4.
∴S△ABC= ![]() basin
basin ![]() =
= ![]() .
.
【解析】(1)利用余弦定理表示出cosC,把已知等式利用正弦定理化简,整理后代入计算求出cosC的值,即可确定出C的度数.(2)设∠ADC=α,则∠CDB=π﹣α.在△ADC与△ADB中,由余弦定理可得:b2+a2=20,在△ABC中,由余弦定理可得:b2+a2+ba=24.可得ba=4.即可得出.
【考点精析】根据题目的已知条件,利用正弦定理的定义和余弦定理的定义的相关知识可以得到问题的答案,需要掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量y(g)与尺寸x(mm)之间近似满足关系式y=axb(a,b为大于0的常数).现随机抽取6件合格产品,测得数据如下:
尺寸(mm) | 38 | 48 | 58 | 68 | 78 | 88 |
质量(g) | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
对数据作了初步处理,相关统计量的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(Ⅰ)根据所给数据,求y关于x的回归方程;
(Ⅱ)按照某项指标测定,当产品质量与尺寸的比在区间( ![]() ,
, ![]() )内时为优等品.现从抽取的6件合格产品中再任选3件,记ξ为取到优等品的件数,试求随机变量ξ的分布列和期望.
)内时为优等品.现从抽取的6件合格产品中再任选3件,记ξ为取到优等品的件数,试求随机变量ξ的分布列和期望.
附:对于一组数据(v1 , u1),(v2 , u2),…,(vn , un),其回归直线u=α+βv的斜率和截距的最小二乘估计分别为 ![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.