题目内容
取棱长为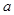 的正方体的一个顶点,过此顶点出发的三条棱的中点作截面,截去正方体的一个角,对正方体的所有顶点都如此操作,则所剩下的多面体:①有12个顶点 ②有24条棱 ③表面积
的正方体的一个顶点,过此顶点出发的三条棱的中点作截面,截去正方体的一个角,对正方体的所有顶点都如此操作,则所剩下的多面体:①有12个顶点 ②有24条棱 ③表面积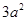 ④体积
④体积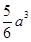
以上结论正确的有________(填上正确的序号).
【答案】
①②④
【解析】
试题分析:截掉一个角能得到3个顶点,而截掉的角的个数为8个,则有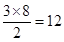 个顶点,故①正确;截掉一个角能得到3条棱,而截掉的角的个数为8个,则有
个顶点,故①正确;截掉一个角能得到3条棱,而截掉的角的个数为8个,则有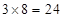 条棱,故②正确;一个截面的面积为
条棱,故②正确;一个截面的面积为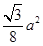 ,则8个截面的面积为
,则8个截面的面积为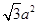 ,另外,还有6个边长为
,另外,还有6个边长为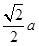 的正方形,求得这6个正方形的面积之和为
的正方形,求得这6个正方形的面积之和为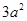 ,则该多面体的表面积为
,则该多面体的表面积为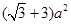 ,故③错误;却去的角为三棱锥,每个三棱锥的体积为
,故③错误;却去的角为三棱锥,每个三棱锥的体积为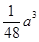 ,则该多面体的体积为
,则该多面体的体积为
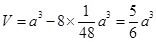 ,故④正确。所以正确的有①②④。
,故④正确。所以正确的有①②④。
考点:棱柱的结构特征
点评:本小题主要考查棱柱的结构特征、多面体的表面积与体积等基础知识,考查运算求解能力,考查空间想象能力、化归与转化思想.属于基础题.

练习册系列答案
相关题目
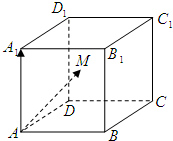 (2013•江门一模)如图,在棱长为2的正方体ABCD-A1B1C1D1内(含正方体表面)任取一点M,则
(2013•江门一模)如图,在棱长为2的正方体ABCD-A1B1C1D1内(含正方体表面)任取一点M,则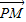 •
•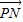 的取值范围是 .
的取值范围是 .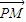 •
•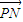 的取值范围是 .
的取值范围是 .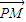 •
•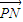 的取值范围是 .
的取值范围是 .