题目内容
（2013•湖州二模）正方体ABCD-A1B1C1D1的棱长为2，MN是它的内切球的一条弦（我们把球面上任意两点之间的线段称为球的弦），P为正方体表面上的动点，当弦MN的长度最大时，
•
的取值范围是
| PM |
| PN |
[0，2]
[0，2]
．分析：根据题意，可设M、N分别是内切球在正方体左、右侧面的切点，运动点P并加以观察，可得当P与正方体的某个顶点重合时，
•
达到最大值；当P与正方体某个面的中心重合时，
•
达到最小值．由此结合数量积的计算公式，即可得到数量积
•
的取值范围．
| PM |
| PN |
| PM |
| PN |
| PM |
| PN |
解答：解：根据题意，MN是正方体内切球的最大弦长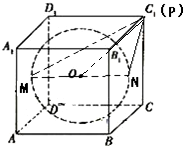
∴MN是内切球的直径
设M、N分别是内切球在正方体左、右侧面的切点，如图
方法1：当P在正方体表面运动，它与正方体的某个顶点重合时，
•
达到最大值．以C1点为例，此时
•
=
•
=
•
cos∠∠MC1N=
2=（
A
）2=2；
当点P与正方体某个面的中心重合时，
•
达到最小值．
此时
⊥
，得
•
=0
综上所述，得数量积
•
的取值范围为[0，2]
方法2：连接PO，可得
•
=（
+
）•（
+
）=
2+
•
+
•
+
•
=
2+
•（
+
）+
•
=
2-1
当|
|达到最大值
时，
•
的最大值为2；当|
|达到最小值1时，
•
的最小值为0．
综上所述，得数量积
•
的取值范围为[0，2]
故答案为：[0，2]
∴MN是内切球的直径
设M、N分别是内切球在正方体左、右侧面的切点，如图
方法1：当P在正方体表面运动，它与正方体的某个顶点重合时，
| PM |
| PN |
| PM |
| PN |
| C1M |
| C1N |
| |C1M| |
| |C1N| |
| |C1N| |
| ||
| 2 |
| A | 1 |
当点P与正方体某个面的中心重合时，
| PM |
| PN |
此时
| PM |
| PN |
| PM |
| PN |
综上所述，得数量积
| PM |
| PN |
方法2：连接PO，可得
| PM |
| PN |
| PO |
| OM |
| PO |
| ON |
| PO |
| PO |
| ON |
| OM |
| PO |
| OM |
| ON |
=
| PO |
| PO |
| ON |
| OM |
| OM |
| ON |
| PO |
当|
| PO |
| 3 |
| PM |
| PN |
| PO |
| PM |
| PN |
综上所述，得数量积
| PM |
| PN |
故答案为：[0，2]
点评：本题给出正方体的内切球，求一个数量积的取值范围．着重考查了平面向量数量积的运算和正方体的性质等知识，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
（2013•湖州二模）已知程序框图如图，则输出的i=