题目内容
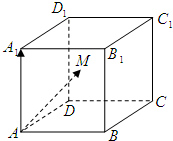 (2013•江门一模)如图,在棱长为2的正方体ABCD-A1B1C1D1内(含正方体表面)任取一点M,则
(2013•江门一模)如图,在棱长为2的正方体ABCD-A1B1C1D1内(含正方体表面)任取一点M,则| AA1 |
| AM |
| 3 |
| 4 |
| 3 |
| 4 |
分析:本题是几何概型问题,欲求点M满足
•
≥1的概率,先以A为原点建立空间直角坐标系,由数量积公式得出点M到平面ABCD的距离大于等于
,点M的轨迹是正方体的
,求出其体积,再根据几何概型概率公式结合正方体的体积的方法求解即可.
| AA1 |
| AM |
| 1 |
| 2 |
| 3 |
| 4 |
解答:解:本题是几何概型问题,正方体的体积为V=8,
以A为原点建立空间直角坐标系,AB为x轴,AD为y轴,AA1为z轴.
那么A(0,0,0),A1(0,0,2)
设M(x,y,z),那么x,y,z∈[0,2]
∴
=(x,y,z),
=(0,0,2)
则
•
≥1,即2z≥1,z≥
.
即点M与平面ABCD的距离大于等于
,点M的轨迹是正方体的
,其体积为:V1=
×8,
则
•
≥1的概率p为:
,
故答案为:
.
以A为原点建立空间直角坐标系,AB为x轴,AD为y轴,AA1为z轴.
那么A(0,0,0),A1(0,0,2)
设M(x,y,z),那么x,y,z∈[0,2]
∴
| AM |
| AA1 |
则
| AA1 |
| AM |
| 1 |
| 2 |
即点M与平面ABCD的距离大于等于
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
则
| AA1 |
| AM |
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:本小题主要考查几何概型、几何概型的应用、几何体的体积等基础知识,考查空间想象能力、化归与转化思想.属于基础题

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目