题目内容
若a>0, b>0, 且函数f(x)=4x3-ax2-2bx+2在x=1处有极值，则ab的最大值等于
- A.2
- B.3
- C.6
- D.9
D
解析：
分析：求出导函数，利用函数在极值点处的导数值为0得到a，b满足的条件；利用基本不等式求出ab的最值；注意利用基本不等式求最值需注意：一正、二定、三相等．
解答：∵f′（x）=12x2-2ax-2b又因为在x=1处有极值∴a+b=6∵a＞0，b＞0∴ab≤(a+b/2)2=9当且仅当a=b=3时取等号所以ab的最大值等于9故选D
点评：本题考查函数在极值点处的导数值为0、考查利用基本不等式求最值需注意：一正、二定、三相等．
解析：
分析：求出导函数，利用函数在极值点处的导数值为0得到a，b满足的条件；利用基本不等式求出ab的最值；注意利用基本不等式求最值需注意：一正、二定、三相等．
解答：∵f′（x）=12x2-2ax-2b又因为在x=1处有极值∴a+b=6∵a＞0，b＞0∴ab≤(a+b/2)2=9当且仅当a=b=3时取等号所以ab的最大值等于9故选D
点评：本题考查函数在极值点处的导数值为0、考查利用基本不等式求最值需注意：一正、二定、三相等．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
p:∃x0∈R,有
-x0+2<0;
+
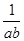的最小值为1.
>1
(B)
+
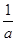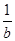≤2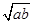
≥1 (D)a2+b2≥2
+
≤
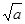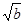;③a2+b2≥2;④a3+b3≥3;⑤
+
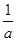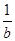≥2.
>
; ②若a>b>0,则a-
>b-
; ③若a>b>0,则
>
;
的最小值为4.