题目内容
4.已知函数f(x)=4cosxcos(x-$\frac{π}{3}$)-2.(I)求函数f(x)的最小正周期;
(II)求函数f(x)在区间[-$\frac{π}{6}$,$\frac{π}{4}$]上的最大值和最小值.
分析 (I)由三角函数公式化简可得f(x)=2sin(2x+$\frac{π}{6}$)-1,由周期公式可得;
(II)由x∈[-$\frac{π}{6}$,$\frac{π}{4}$]可得2x+$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{2π}{3}$],由三角函数的性质可得最值.
解答 解:(I)由三角函数公式化简可得f(x)=4cosxcos(x-$\frac{π}{3}$)-2
=4cosx($\frac{1}{2}$cosx+$\frac{\sqrt{3}}{2}$sinx)-2=$\sqrt{3}$sin2x+2cos2x-2
=$\sqrt{3}$sin2x+cos2x-1=2sin(2x+$\frac{π}{6}$)-1,
∴函数f(x)的最小正周期T=$\frac{2π}{2}$=π;
(II)∵x∈[-$\frac{π}{6}$,$\frac{π}{4}$],∴2x+$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{2π}{3}$],
∴当2x+$\frac{π}{6}$=$\frac{π}{2}$即x=$\frac{π}{6}$时,f(x)取最大值1;
当2x+$\frac{π}{6}$=-$\frac{π}{6}$即x=-$\frac{π}{6}$时,f(x)取最小值-2.
点评 本题考查三角函数的最值,涉及三角函数的周期性和三角函数公式,属基础题.

练习册系列答案
相关题目
12.i为虚数单位,若复数z与(z+2)2-8i都是纯虚数,则z=( )
| A. | 2 | B. | -2 | C. | -2i | D. | 2i |
9.已知向量$\overrightarrow{a}$=(1,1,0),$\overrightarrow{b}$=(-1,0,2)且k$\overrightarrow{a}$+$\overrightarrow{b}$与2$\overrightarrow{a}$-$\overrightarrow{b}$互相垂直,则k的值是( )
| A. | 1 | B. | $\frac{1}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{7}{5}$ |
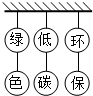 2012年10月18日全国第二届绿色运动会在池洲隆垦开幕.本次大会的主题是“绿色、低碳、环保”为大力宣传这一主题,主办方将这6个字做成灯笼悬挂在主会场(如图所示),大会结束后,要将这6个灯笼撤下来,每次撤其中一列最下面的一个,则不同的撤法种数为( )
2012年10月18日全国第二届绿色运动会在池洲隆垦开幕.本次大会的主题是“绿色、低碳、环保”为大力宣传这一主题,主办方将这6个字做成灯笼悬挂在主会场(如图所示),大会结束后,要将这6个灯笼撤下来,每次撤其中一列最下面的一个,则不同的撤法种数为( )