题目内容
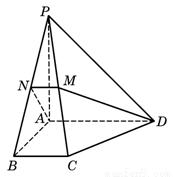
(本题8分)如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为正方形,
PA=AB=2,M, N分别为PA, BC的中点.
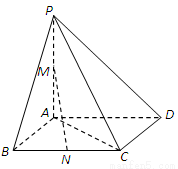
(Ⅰ)证明:MN∥平面PCD;
(Ⅱ)求MN与平面PAC所成角的正切值.
【答案】
(Ⅰ)见解析;(Ⅱ)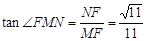 .
.
【解析】(I)取AD的中点E,连接NE,ME,易证: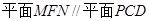 .
.
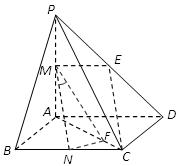
(II)找出(做)线面角是解题的关键.因为平面PAC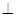 平面ABCD,所以过N作NF⊥AC于F,连接MF .所以NF⊥平面PAC, ∴∠FMN是MN与平面PAC所成的角.
平面ABCD,所以过N作NF⊥AC于F,连接MF .所以NF⊥平面PAC, ∴∠FMN是MN与平面PAC所成的角.
(Ⅰ)取PD的中点E,连接ME, CE.
∵M, N分别为PA, BC的中点,
∴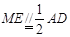 ,
,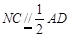 ,∴
,∴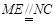 ,
,
∴MNCE是平行四边形,∴MN∥CE,……………2分
∵CEÍ平面PCD,MNË平面PCD,
∴MN∥平面PCD.…………………………………2分
(Ⅱ)作NF⊥AC于F,连接MF.
∵PA⊥平面ABCD,∴PA⊥NF,又∵PA∩AC=A,
∴NF⊥平面PAC,∴∠FMN是MN与平面PAC所成的角.………2分
在Rt△MFN中,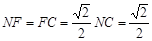 ,
,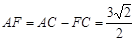 ,
,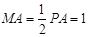 ,
,
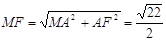 ,
,
∴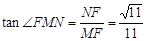 .……………………………………………2分
.……………………………………………2分

练习册系列答案
相关题目
 中,
中, 是
是 的中点,
的中点,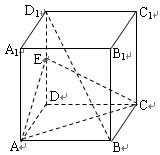
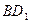 ∥平面
∥平面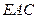 ;
;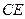 所成角的余弦值.
所成角的余弦值. 中,
中, 底面
底面 ,
, 分
分 的中点,求证:
的中点,求证: 平面
平面 ;
; 平面
平面 .高.考.资.源.网
.高.考.资.源.网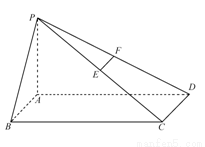
 中,底面为直角梯形,
中,底面为直角梯形,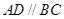 ,
, 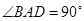 ,
,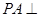 底面
底面 ,且
,且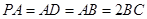 ,
,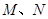 分别为
分别为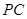 、
、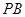 的中点。
的中点。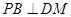 ;
;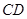 与平面
与平面 所成角的正弦值。
所成角的正弦值。
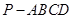 中,底面为直角梯形,
中,底面为直角梯形,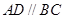 ,
,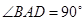 ,
,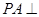 底面
底面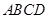 ,且
,且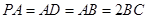 ,
,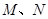 分别为
分别为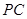 、
、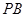 的中点。
的中点。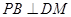 ;
;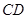 与平面
与平面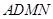 所成角的正弦值。
所成角的正弦值。