题目内容
解答题
已知椭圆的两焦点为F1(－1，0)、F2(1，0)，P为椭圆上一点，且2|F1F2|＝|PF1|＋|PF2|．
(1)求此椭圆的方程；
(2)若∠F1PF2＝
，求△PF1F2的面积．
答案：
解析：
解析：
|
(1)由题知|PF1|＋|PF2|＝4，∴2a＝4，∴a＝2． 又 c＝1，∴b2＝3．∴椭圆方程为 ＋ ＝1．
(2)设|PF1|＝m，|PF2|＝n，则有
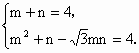
即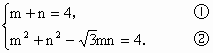 
①式平方得 m2＋n2＋2mn＝16，减去②式得(2＋ )mn＝12，
∴ mn＝ ＝12(2－ )．
∴ S＝ mn ＝3(2－ )．
|
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
(0，－
)，对应准线是y＝－
，并且
和
的等比中项是离心率e．
平分，试求直线l的倾斜角的取值范围．
(0，－1)和
(0，1)，直线y＝4是该椭圆的一条准线．
＝1，求tan∠
)、F2(0，2
)，离心率为
，(1)求椭圆的方程；(2)若一条不与坐标轴平行的直线l与此椭圆交于不同的两点M、N，且线段MN的中点的横坐标为－
，求直线l的倾斜角的取值范围．