题目内容
已知椭圆的两焦点 (0,-1)和
(0,-1)和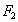 (0,1),直线y=4是该椭圆的一条准线.
(0,1),直线y=4是该椭圆的一条准线.
(1)求椭圆的方程;
(2)已知椭圆上一点P满足 =1,求tan∠
=1,求tan∠ P
P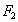 .
.
答案:

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
题目内容
已知椭圆的两焦点 (0,-1)和
(0,-1)和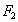 (0,1),直线y=4是该椭圆的一条准线.
(0,1),直线y=4是该椭圆的一条准线.
(1)求椭圆的方程;
(2)已知椭圆上一点P满足 =1,求tan∠
=1,求tan∠ P
P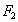 .
.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案