题目内容
解答题
已知椭圆的两个焦点分别为F1(0，－2
)、F2(0，2
)，离心率为
，(1)求椭圆的方程；(2)若一条不与坐标轴平行的直线l与此椭圆交于不同的两点M、N，且线段MN的中点的横坐标为－
，求直线l的倾斜角的取值范围．
答案：
解析：
解析：
|
①设椭圆方程为 又e＝ ②设直线l的方程为y＝kx＋b(k≠0)，代入椭圆方程，得(k2＋9)x2＋2kbx＋b2－9＝0． ∴x1＋x2＝ ∴b＝ ∵Δ＞0， ∴(2kb)2－4(k2＋9)(b2－9)＞0． ∴k4＋6k2－27＞0，解得k2＞3， ∴k＞ 又倾角不等于 |
＋
＝1(a＞b＞0)，依题有c＝2
，
．∴a＝3，∴b＝1．∴椭圆方程为
＋x2＝1．
＝－1．
．
或k＜－
．
，∴倾角的取值范围是(
，
)∪(
，
)．
练习册系列答案
相关题目
(0，－
)，对应准线是y＝－
，并且
和
的等比中项是离心率e．
平分，试求直线l的倾斜角的取值范围．
，求△PF1F2的面积．
(0，－1)和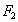
(0，1)，直线y＝4是该椭圆的一条准线．
＝1，求tan∠