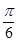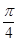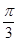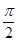题目内容
(12分)在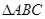 中,角
中,角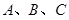 的对边分别为
的对边分别为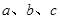 ,且
,且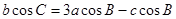 .
.
①求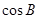 的值;
的值;
②若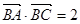 ,且
,且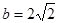 ,求
,求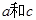 的值.
的值.
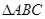 中,角
中,角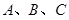 的对边分别为
的对边分别为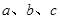 ,且
,且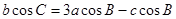 .
.①求
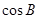 的值;
的值;②若
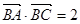 ,且
,且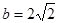 ,求
,求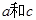 的值.
的值.(Ⅰ)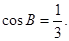 (Ⅱ)
(Ⅱ) 
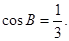 (Ⅱ)
(Ⅱ) 
试题分析:(1)第一问中根据正弦定理,化边为角,结合内角和定理,得到cosB
(2)由于利用数量积公式
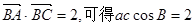 ,那么根据第一问的角B的余弦值,结合余弦定理得到关于a,c的方程得到求解。
,那么根据第一问的角B的余弦值,结合余弦定理得到关于a,c的方程得到求解。(Ⅰ)解:由正弦定理得
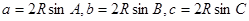 ,
, 因此
因此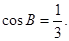 ………6分
………6分(Ⅱ)解:由
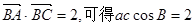 ,
,
所以
 ………12分
………12分点评:解决该试题的关键是合理使用正弦定理化边为角,得到三角函数关系式,然后得到结论。也可以通过余弦定理化角为边,得到三边的平方关系式,得到角B的余弦值。

练习册系列答案
相关题目
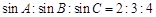 ,那么cosC等于 ( )
,那么cosC等于 ( )
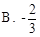
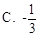
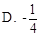
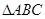 中,
中,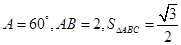 ,则
,则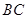 的长为( )
的长为( )
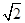 n mile的位置B,经过40分钟又测得该船已行驶到点A北偏东
n mile的位置B,经过40分钟又测得该船已行驶到点A北偏东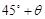 (其中
(其中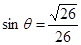 ,
,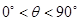 )且与点A相距10
)且与点A相距10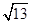 n mile的位置C.
n mile的位置C.
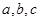 且
且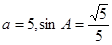 .
.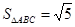 ,求周长的最小值; (Ⅱ) 若
,求周长的最小值; (Ⅱ) 若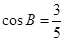 ,求边
,求边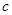 的值.
的值. 中,
中, 为
为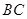 中点,
中点,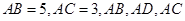 成等比数列,则
成等比数列,则 中,已知
中,已知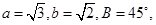 求
求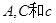 .
.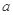 、b、c ,若(
、b、c ,若(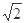 b – c)cosA=acosC,则cosA=______
b – c)cosA=acosC,则cosA=______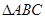 中,若
中,若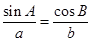 ,则角B为( )
,则角B为( )