题目内容
(本小题满分12分)
已知△ABC的内角A、B、C所对的边分别为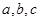 且
且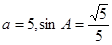 .
.
( I ) 若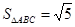 ,求周长的最小值; (Ⅱ) 若
,求周长的最小值; (Ⅱ) 若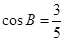 ,求边
,求边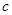 的值.
的值.
已知△ABC的内角A、B、C所对的边分别为
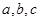 且
且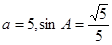 .
.( I ) 若
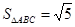 ,求周长的最小值; (Ⅱ) 若
,求周长的最小值; (Ⅱ) 若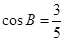 ,求边
,求边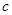 的值.
的值.解:(1)当且仅当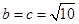 时,周长取到最小值为
时,周长取到最小值为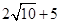 ;(2)
;(2)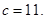
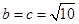 时,周长取到最小值为
时,周长取到最小值为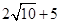 ;(2)
;(2)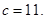
试题分析:(1)根据三角形的面积公式和已知条件得到
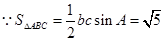 ,
,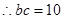 然后表示出周长l,结合均值不得等式得到最值。
然后表示出周长l,结合均值不得等式得到最值。(2) ∵cosB=
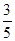 >0,且0<B<π,结合同角公式得到sinB,由正弦定理得
>0,且0<B<π,结合同角公式得到sinB,由正弦定理得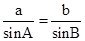 ,
,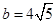
解:(1)
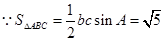 ,
,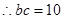 ,
,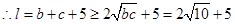 ,
,当且仅当
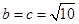 时,周长取到最小值为
时,周长取到最小值为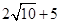
(2) ∵cosB=
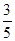 >0,且0<B<π,∴sinB=
>0,且0<B<π,∴sinB=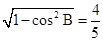
由正弦定理得
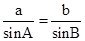 ,
,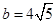 ;
; 再由余弦定理得:
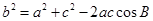 即
即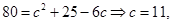 或
或 (舍去)
(舍去)点评:解决该试题的关键是通过均值不等式得到周长的最小值。

练习册系列答案
相关题目
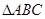 中,
中,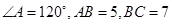 ,则
,则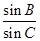 的值为___________.
的值为___________.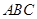 中,
中,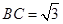 ,
,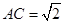 ,
,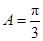 ,则
,则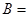 .
. 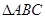 中,若
中,若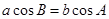 ,则
,则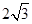 ,点D 在BC边上,∠ADC=45°,则AD的长度等于______.
,点D 在BC边上,∠ADC=45°,则AD的长度等于______.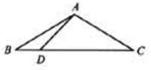
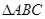 中,角
中,角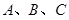 的对边分别为
的对边分别为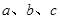 ,且
,且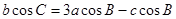 .
.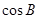 的值;
的值;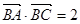 ,且
,且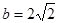 ,求
,求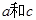 的值.
的值.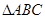 中,
中,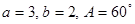 ,求
,求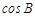 及
及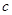 的值.
的值.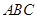 中
中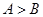 ,给出下列不等式:
,给出下列不等式: 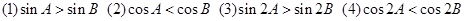
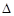 ABC中,已知
ABC中,已知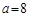 ,
,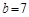 ,
,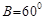 ,求
,求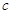 .
.