题目内容
我们将具有下列性质的所有函数组成集合M:函数y=f(x)(x∈D),对任意x,y,![]() 均满足f(
均满足f(![]() )≥
)≥![]() [f(x)+f(y)],当且仅当x=y时等号成立.
[f(x)+f(y)],当且仅当x=y时等号成立.
若定义在(0,+∞)上的函数f(x)∈M,试比较f(3)+f(5)与2f(4)大小.
给定两个函数:f1(x)=![]() (x>0),f2(x)=logax(a>1,x>0).
(x>0),f2(x)=logax(a>1,x>0).
证明:f1(x)![]() M,f2(x)∈M.
M,f2(x)∈M.
试利用(2)的结论解决下列问题:若实数m、n满足2m+2n=1,求m+n的最大值.
答案:
解析:
解析:
|
得 当且仅当 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

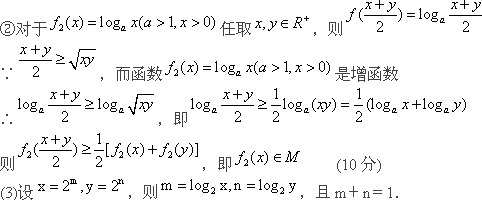
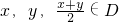 均满足
均满足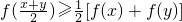 ,当且仅当x=y时等号成立.
,当且仅当x=y时等号成立. 均满足
均满足 ,当且仅当x=y时等号成立.
,当且仅当x=y时等号成立. ,f2(x)=logax(a>1,x>0).证明:f1(x)∉M,f2(x)∈M.
,f2(x)=logax(a>1,x>0).证明:f1(x)∉M,f2(x)∈M.