题目内容
我们将具有下列性质的所有函数组成集合M:函数y=f(x)(x∈D),对任意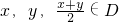 均满足
均满足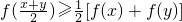 ,当且仅当x=y时等号成立.
,当且仅当x=y时等号成立.
(1)若定义在(0,+∞)上的函数f(x)∈M,试比较f(3)+f(5)与2f(4)大小.
(2)设函数g(x)=-x2,求证:g(x)∈M.
(3)已知函数f(x)=log2x∈M.试利用此结论解决下列问题:若实数m、n满足2m+2n=1,求m+n的最大值.
解:(1) ,即f(3)+f(5)≤2f(4)
,即f(3)+f(5)≤2f(4)
但3≠5,所以f(3)+f(5)<2f(4)
(若答案写成f(3)+f(5)≤2f(4),扣一分) (4分)
(2)任取x,y∈R,则 ,
, ,(6分)
,(6分)
所以 ,
,
当且仅当x=y时等号成立,则g(x)∈M.(10分)
(3)设x=2m,y=2n,则m=log2x,n=log2y.
由已知:函数f(x)=log2x满足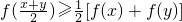
得 ,即
,即 ,则m+n≤-2(14分)
,则m+n≤-2(14分)
当且仅当x=y,即 ,即m=n=-1时,m+n有最大值为-2.(16分)
,即m=n=-1时,m+n有最大值为-2.(16分)
分析:(1)根据对任意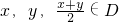 均满足
均满足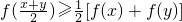 可得
可得 ,化简可得结论;
,化简可得结论;
(2)任取x,y∈R,然后计算 的符号,从而判定是否满足定义;
的符号,从而判定是否满足定义;
(3)设x=2m,y=2n,则m=log2x,n=log2y,且m+n=1,而函数f(x)=log2x满足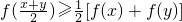 建立关系式可求出m+n的最大值.
建立关系式可求出m+n的最大值.
点评:本题主要考查了抽象函数的性质,以及基本不等式研究函数的最值,属于中档题.
 ,即f(3)+f(5)≤2f(4)
,即f(3)+f(5)≤2f(4)但3≠5,所以f(3)+f(5)<2f(4)
(若答案写成f(3)+f(5)≤2f(4),扣一分) (4分)
(2)任取x,y∈R,则
 ,
, ,(6分)
,(6分)所以
 ,
,当且仅当x=y时等号成立,则g(x)∈M.(10分)
(3)设x=2m,y=2n,则m=log2x,n=log2y.
由已知:函数f(x)=log2x满足
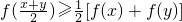
得
 ,即
,即 ,则m+n≤-2(14分)
,则m+n≤-2(14分)当且仅当x=y,即
 ,即m=n=-1时,m+n有最大值为-2.(16分)
,即m=n=-1时,m+n有最大值为-2.(16分)分析:(1)根据对任意
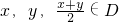 均满足
均满足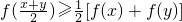 可得
可得 ,化简可得结论;
,化简可得结论;(2)任取x,y∈R,然后计算
 的符号,从而判定是否满足定义;
的符号,从而判定是否满足定义;(3)设x=2m,y=2n,则m=log2x,n=log2y,且m+n=1,而函数f(x)=log2x满足
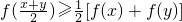 建立关系式可求出m+n的最大值.
建立关系式可求出m+n的最大值.点评:本题主要考查了抽象函数的性质,以及基本不等式研究函数的最值,属于中档题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
 均满足
均满足 ,当且仅当x=y时等号成立.
,当且仅当x=y时等号成立. ,f2(x)=logax(a>1,x>0).证明:f1(x)∉M,f2(x)∈M.
,f2(x)=logax(a>1,x>0).证明:f1(x)∉M,f2(x)∈M.