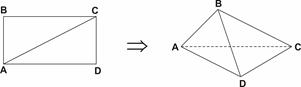
题目内容
(本小题满分14分)
如图,在直三棱柱ABC-A1B1C1中,已知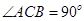 ,M为A1B与AB1的交点,N为棱B1C1的中点
,M为A1B与AB1的交点,N为棱B1C1的中点

(1) 求证:MN∥平面AA1C1C
(2) 若AC=AA1,求证:MN⊥平面A1BC
如图,在直三棱柱ABC-A1B1C1中,已知
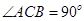 ,M为A1B与AB1的交点,N为棱B1C1的中点
,M为A1B与AB1的交点,N为棱B1C1的中点
(1) 求证:MN∥平面AA1C1C
(2) 若AC=AA1,求证:MN⊥平面A1BC
见解析。
本试题主要是考查了线面平行的证明与线面垂直的证明的综合运用。
(1)线面平行的证明关键是证明线线平行,结合判定定理得到结论。
(2)对于线面垂直的判定,我们可以利用线线垂直,如果一个平面内的一条直线垂直于某个平面内的任意两条相交直线,则线面垂直的定理得到。
⑴连接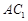 ,因为
,因为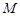 为
为 与
与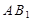 的交点,所以
的交点,所以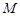 是
是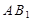 的中点,又
的中点,又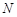 为棱
为棱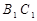 的中点.所以
的中点.所以 ∥
∥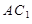 ,………………………4分
,………………………4分
又因为 平面
平面 ,
, 平面
平面 ,
,
所以 ∥平面
∥平面 . …………………………6分
. …………………………6分

⑵ 因为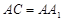 ,所以四边形
,所以四边形 是正方形,
是正方形,
所以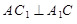 ,又因为
,又因为 是直三棱柱,
是直三棱柱,
所以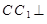 平面
平面 ,
,
因为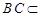 平面
平面 ,所以
,所以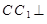
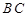 .
.
又因为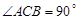 ,所以
,所以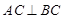 ,
,
因为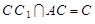 ,所以
,所以 平面
平面 ,
,
所以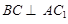 ,又
,又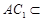 平面
平面 ,………………………………………………8分
,………………………………………………8分
因为 ∥
∥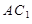 ,所以
,所以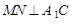 ,
,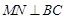 , ………………………………10分
, ………………………………10分
又 ,所以
,所以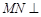 平面
平面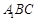 .……………………………………………14分
.……………………………………………14分
(1)线面平行的证明关键是证明线线平行,结合判定定理得到结论。
(2)对于线面垂直的判定,我们可以利用线线垂直,如果一个平面内的一条直线垂直于某个平面内的任意两条相交直线,则线面垂直的定理得到。
⑴连接
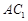 ,因为
,因为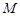 为
为 与
与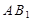 的交点,所以
的交点,所以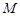 是
是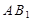 的中点,又
的中点,又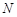 为棱
为棱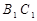 的中点.所以
的中点.所以 ∥
∥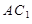 ,………………………4分
,………………………4分又因为
 平面
平面 ,
, 平面
平面 ,
,所以
 ∥平面
∥平面 . …………………………6分
. …………………………6分
⑵ 因为
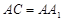 ,所以四边形
,所以四边形 是正方形,
是正方形,所以
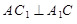 ,又因为
,又因为 是直三棱柱,
是直三棱柱,所以
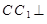 平面
平面 ,
,因为
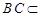 平面
平面 ,所以
,所以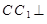
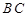 .
.又因为
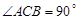 ,所以
,所以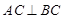 ,
,因为
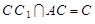 ,所以
,所以 平面
平面 ,
,所以
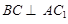 ,又
,又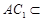 平面
平面 ,………………………………………………8分
,………………………………………………8分因为
 ∥
∥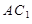 ,所以
,所以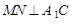 ,
,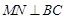 , ………………………………10分
, ………………………………10分又
 ,所以
,所以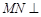 平面
平面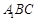 .……………………………………………14分
.……………………………………………14分
练习册系列答案
相关题目
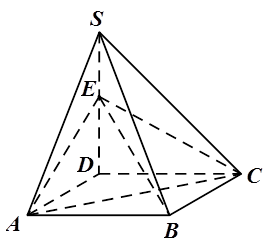
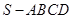 的底面是正方形,
的底面是正方形, ⊥平面
⊥平面 ,
, ,点E
,点E .
.
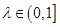 ,都有AC⊥BE;
,都有AC⊥BE; ,求
,求 的值.
的值.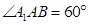 , M是A1B1的中点,
, M是A1B1的中点,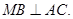

 平面ABC;
平面ABC;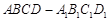 中,
中,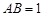 ,
,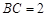 ,
,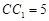 ,
,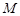 为棱
为棱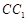 上一点.
上一点.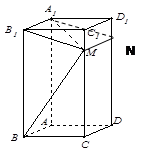
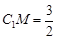 ,求异面直线
,求异面直线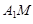 和
和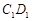 所成角的正切值;
所成角的正切值;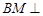 平面
平面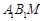 ?若存在,求出
?若存在,求出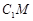 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.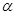 ,则
,则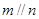
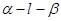 是直二面角,若直线
是直二面角,若直线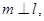 则
则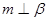
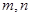 在平面
在平面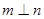 ,则
,则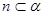 或
或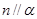
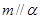 ,则n与
,则n与 是不同的直线,
是不同的直线, 是不同的平面,则下列结论错误的是( )
是不同的平面,则下列结论错误的是( )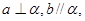 则
则
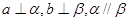 ,则
,则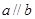
 ,则
,则
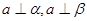 ,则
,则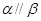
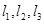 是空间三条不同的直线,则下列命题正确的是( )
是空间三条不同的直线,则下列命题正确的是( )
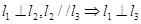
 共面
共面 共面
共面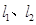 为异面直线,直线
为异面直线,直线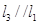 ,则
,则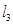 与
与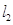 的位置关系是
的位置关系是