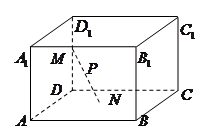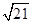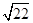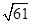题目内容
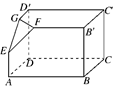
如图, 在正方体ABCD—A1B1C1D1中,E,F分别是正方形A1B1C1D1和ADD1A1的中心,则EF和BD所成的角是 。

60°
试题分析:由于根据题意可知,E,F分别是正方形A1B1C1D1和ADD1A1的中心,因为B1D1//BD,则异面直线EF和BD所成的角是B1D1与EF所成的夹角。在三角形EFD1中,设正方体的棱长为1,则EF=FD1= ED1 =
 ,根据余弦定理可知得到cos D1EF=
,根据余弦定理可知得到cos D1EF=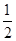 ,可知其结论为60°,故答案为60°。
,可知其结论为60°,故答案为60°。点评:解决该试题的关键是利用平移法来转换为相交直线的夹角来得到异面直线的所成的角的求解的问题的运用。

练习册系列答案
相关题目

 ,高为
,高为 ,则圆锥的侧面积是
,则圆锥的侧面积是  .
.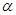 的一条斜线,O为斜足,OB为OA在平面
的一条斜线,O为斜足,OB为OA在平面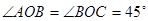 ,则
,则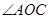 的大小为( )
的大小为( )



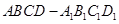 的棱长为
的棱长为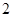 ,长为
,长为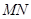 的一个端点
的一个端点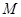 在棱
在棱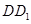 上运动,点
上运动,点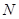 在正方形
在正方形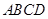 内运动,则
内运动,则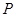 的轨迹的面积为( )
的轨迹的面积为( )