题目内容
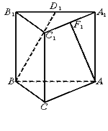
如图,已知正方体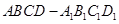 的棱长为
的棱长为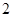 ,长为
,长为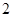 的线段
的线段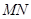 的一个端点
的一个端点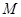 在棱
在棱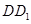 上运动,点
上运动,点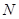 在正方形
在正方形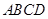 内运动,则
内运动,则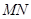 中点
中点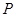 的轨迹的面积为( )
的轨迹的面积为( )
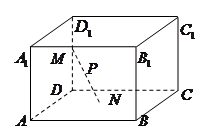
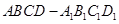 的棱长为
的棱长为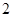 ,长为
,长为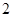 的线段
的线段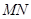 的一个端点
的一个端点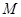 在棱
在棱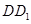 上运动,点
上运动,点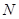 在正方形
在正方形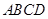 内运动,则
内运动,则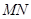 中点
中点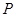 的轨迹的面积为( )
的轨迹的面积为( )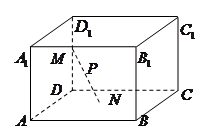
A.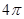 | B.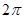 | C.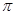 | D.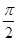 |
D
本试题主要是考查了立体几何中点的轨迹的求解问题。
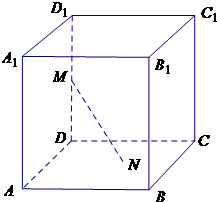
如图可得,端点N在正方形ABCD内运动,连接N点与D点,
由ND,DM,MN构成一个直角三角形,
设P为MN的中点,根据直角三角形斜边上的中线长度为斜边的一半可得,不论△MDN如何变化,P点到D点的距离始终等于1.故P点的轨迹是一个以D为中心,半径为1的球的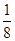 球面积,所以答案为
球面积,所以答案为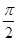 ,故选D.
,故选D.
解决该试题的关键是根据直角三角形斜边上的中线长度为斜边的一半可得,不论△MDN如何变化,P点到D点的距离始终等于1。

如图可得,端点N在正方形ABCD内运动,连接N点与D点,
由ND,DM,MN构成一个直角三角形,
设P为MN的中点,根据直角三角形斜边上的中线长度为斜边的一半可得,不论△MDN如何变化,P点到D点的距离始终等于1.故P点的轨迹是一个以D为中心,半径为1的球的
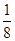 球面积,所以答案为
球面积,所以答案为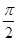 ,故选D.
,故选D.解决该试题的关键是根据直角三角形斜边上的中线长度为斜边的一半可得,不论△MDN如何变化,P点到D点的距离始终等于1。

练习册系列答案
相关题目
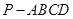 底面ABCD是矩形,PA⊥平面ABCD, AD=2,AB=1,E.F
底面ABCD是矩形,PA⊥平面ABCD, AD=2,AB=1,E.F
 与平面
与平面 所成的角为
所成的角为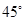 ,求二面角
,求二面角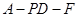 的余弦值.
的余弦值.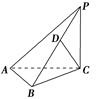
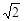 ,则此四面体体积的最大值是
,则此四面体体积的最大值是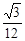
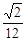
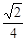
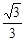

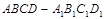 的八个顶点中,平面
的八个顶点中,平面 经过其中的四个顶点,其余四个顶点到平面
经过其中的四个顶点,其余四个顶点到平面