题目内容
设各项均为正数的数列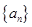 的前
的前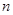 项和为
项和为 ,且
,且 满足
满足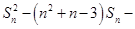
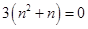 ,
, .
.
(1)求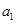 的值;
的值;
(2)求数列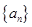 的通项公式;
的通项公式;
(3)证明:对一切正整数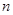 ,有
,有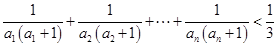 .
.
(1)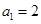 ;(2)
;(2)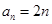 ;(3)详见解析.
;(3)详见解析.
解析试题分析:(1)将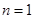 代入方程
代入方程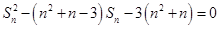 得到
得到 ,结合题中条件(数列
,结合题中条件(数列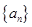 的各项均为正数,得到
的各项均为正数,得到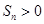 )求出
)求出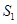 的值,从而得到
的值,从而得到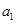 的值;(2)由十字相乘法结合
的值;(2)由十字相乘法结合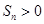 得到
得到 的表达式,然后在
的表达式,然后在 的情况下,由
的情况下,由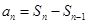 求出数列
求出数列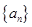 的表达式,并验证
的表达式,并验证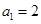 是否满足该表达式,从而得到数列
是否满足该表达式,从而得到数列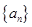 的通项公式;(3)解法一是利用放缩法得到
的通项公式;(3)解法一是利用放缩法得到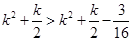
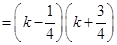 ,于是得到
,于是得到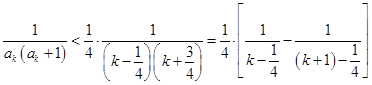 ,最后利用裂项求和法证明题中的不等式;解法二是保持
,最后利用裂项求和法证明题中的不等式;解法二是保持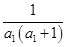 不放缩,在
不放缩,在 的条件下放缩为
的条件下放缩为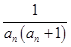
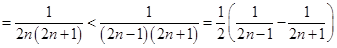 ,最后在
,最后在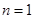 和
和 时利用放缩法结合裂项法证明相应的不等式.
时利用放缩法结合裂项法证明相应的不等式.
(1)令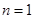 得:
得: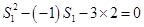 ,即
,即 ,
,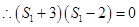 ,
, ,
,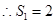 ,即
,即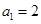 ;
;
(2)由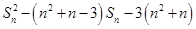 ,得
,得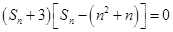 ,
,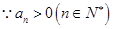 ,
,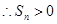 ,从而
,从而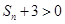 ,
,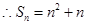 ,
,
所以当 时,
时,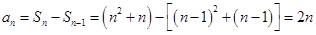 ,
,
又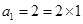 ,
,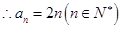 ;
;
(3)解法一:当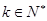 时,
时, ,
,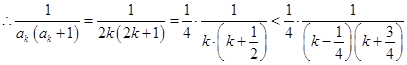
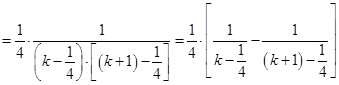
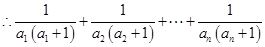
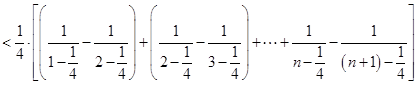
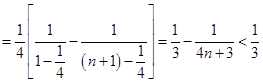 .
.
证法二:当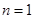 时,
时,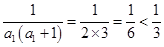 成立,
成立,
当 时,
时,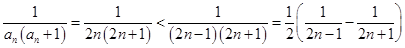 ,
,
则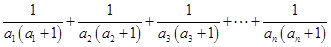
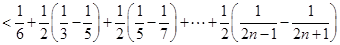
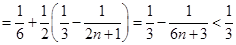 .
.
考点:本题以二次方程的形式以及 与
与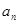 的关系考查数列通项的求解,以及利用放缩法证明数列不等式的综合问题,考查学生的计算能力与逻辑推理能力,属于中等偏难题.
的关系考查数列通项的求解,以及利用放缩法证明数列不等式的综合问题,考查学生的计算能力与逻辑推理能力,属于中等偏难题.

练习册系列答案
相关题目
 的前
的前 项和
项和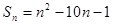
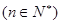 ,则此数列的通项公式为 .
,则此数列的通项公式为 .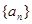 的各项均为正数,
的各项均为正数,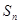 是数列
是数列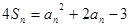 .
.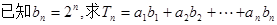 的值.
的值. 的前
的前 项和为
项和为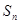 ,对任意的正整数
,对任意的正整数 成立,记
成立,记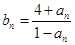 .(1)(1)求数列
.(1)(1)求数列 的通项公式;
的通项公式;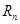 ,是否存在正整数
,是否存在正整数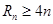 成立?若存在,找出一个正整数
成立?若存在,找出一个正整数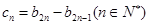 ,设数列
,设数列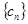 的前
的前 ,求证:对于
,求证:对于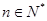 都有
都有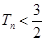
 是公差不为零的等差数列,
是公差不为零的等差数列,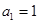 ,且
,且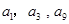 成等比数列.
成等比数列.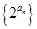 的前
的前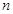 项和
项和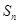 .
.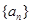 的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.数列
的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.数列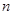 项和为
项和为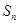 ,且满足
,且满足
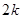 项和
项和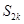 ;
;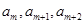 ,按原来的顺序成等差数列?若存在,求出所有满足条件的正整数
,按原来的顺序成等差数列?若存在,求出所有满足条件的正整数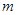 的值;若不存在,说明理由.
的值;若不存在,说明理由.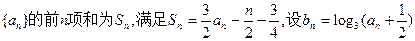 ,则数列
,则数列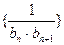 的前19项和为
的前19项和为 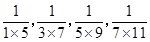 ,…
,… ,…
,…