题目内容
已知二阶矩阵M有特征值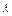 =8及对应的一个特征向量e1=
=8及对应的一个特征向量e1=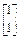 ,并且矩阵M对应的变换将点(-1,2)变换成(-2,4).
,并且矩阵M对应的变换将点(-1,2)变换成(-2,4).
(1)求矩阵M;
(2)求矩阵M的另一个特征值及对应的一个特征向量e2的坐标之间的关系.
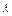 =8及对应的一个特征向量e1=
=8及对应的一个特征向量e1=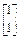 ,并且矩阵M对应的变换将点(-1,2)变换成(-2,4).
,并且矩阵M对应的变换将点(-1,2)变换成(-2,4).(1)求矩阵M;
(2)求矩阵M的另一个特征值及对应的一个特征向量e2的坐标之间的关系.
(1)M=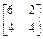 (2)矩阵M的另一个特征值对应的特征向量的坐标之间的关系是2x+y=0
(2)矩阵M的另一个特征值对应的特征向量的坐标之间的关系是2x+y=0
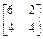 (2)矩阵M的另一个特征值对应的特征向量的坐标之间的关系是2x+y=0
(2)矩阵M的另一个特征值对应的特征向量的坐标之间的关系是2x+y=0(1)设M=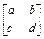 ,则
,则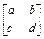
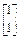 =8
=8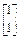 =
=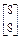 ,
,
故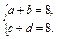 2分
2分
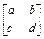
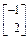 =
=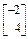 ,故
,故 4分
4分
联立以上两方程组解得a=6,b=2,c=4,d=4,
故M=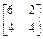 . 6分
. 6分
(2)由(1)知,矩阵M的特征多项式为f(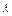 )=(
)=(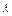 -6)(
-6)(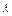 -4)-8=
-4)-8=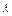 2-10
2-10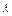 +16,
+16,
故其另一个特征值为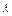 ="2. " 9分
="2. " 9分
设矩阵M的另一个特征向量是e2=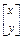 ,
,
则Me2=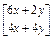 =2
=2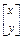 ,所以
,所以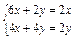 , 12分
, 12分
所以矩阵M的另一个特征值对应的特征向量的坐标之间的关系是2x+y="0. " 14分
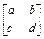 ,则
,则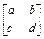
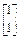 =8
=8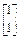 =
=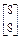 ,
,故
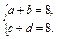 2分
2分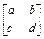
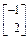 =
=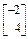 ,故
,故 4分
4分联立以上两方程组解得a=6,b=2,c=4,d=4,
故M=
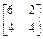 . 6分
. 6分(2)由(1)知,矩阵M的特征多项式为f(
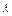 )=(
)=(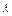 -6)(
-6)(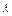 -4)-8=
-4)-8=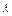 2-10
2-10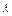 +16,
+16,故其另一个特征值为
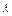 ="2. " 9分
="2. " 9分设矩阵M的另一个特征向量是e2=
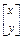 ,
,则Me2=
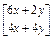 =2
=2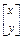 ,所以
,所以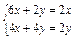 , 12分
, 12分所以矩阵M的另一个特征值对应的特征向量的坐标之间的关系是2x+y="0. " 14分

练习册系列答案
相关题目
 ,则其对应的方程组为_____________
,则其对应的方程组为_____________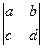 为二阶行列式,并规定
为二阶行列式,并规定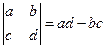 。已知复数z满足
。已知复数z满足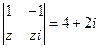 (i为虚数单位),则|z-3i|= 。
(i为虚数单位),则|z-3i|= 。 个数
个数 ,
,
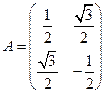 ,求矩阵A的特征向量及A2
,求矩阵A的特征向量及A2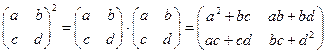 ,则
,则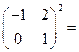 __________.
__________.