题目内容
已知函数 ,
, ,
,
(1)若 为奇函数,求
为奇函数,求 的值;
的值;
(2)若 =1,试证
=1,试证 在区间
在区间 上是减函数;
上是减函数;
(3)若 =1,试求
=1,试求 在区间
在区间 上的最小值.
上的最小值.
(1)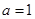
(2)利用“定义法”证明。 在区间
在区间 上是减函数
上是减函数
(3) 若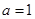 ,由(2)知
,由(2)知 在区间
在区间 上是减函数,在区间
上是减函数,在区间 上,当
上,当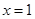 时,
时,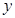 有最小值,且最小值为2。
有最小值,且最小值为2。
解析试题分析:(1)当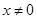 时,
时,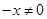 ,若
,若 为奇函数,则
为奇函数,则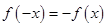
即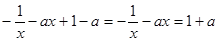 ,所以
,所以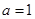
(2)若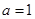 ,则
,则 =
=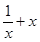
设为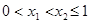 ,
, 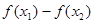 =
=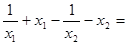
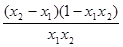
∵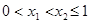
∴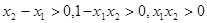 ,∴
,∴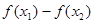 >0
>0
所以,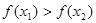 ,因此
,因此 在区间
在区间 上是减函数
上是减函数
(3) 若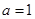 ,由(2)知
,由(2)知 在区间
在区间 上是减函数,下面证明
上是减函数,下面证明 在区间
在区间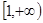 上是增函数.
上是增函数.
设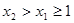 ,
, 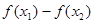 =
=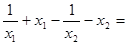
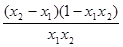
∵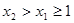 ,
,
∴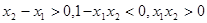
∴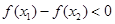
所以 ,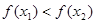
因此 在区间上
在区间上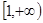 上是增函数
上是增函数
因此,在区间 上,当
上,当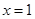 时,
时,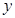 有最小值,且最小值为2
有最小值,且最小值为2
考点:函数的奇偶性、单调性及其应用
点评:中档题,研究函数的奇偶性,要注意定义域关于原点对称。利用定义法研究函数的单调性,要注意遵循“设,作差,变形,定号,结论”等步骤,关键是变形与定号。函数的单调性的基本应用之一是求函数的最值。

练习册系列答案
相关题目
 是定义在
是定义在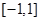 上的奇函数,且
上的奇函数,且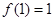 ,若
,若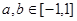 ,
,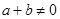 有
有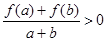 恒成立.
恒成立.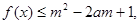 对所有
对所有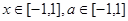 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。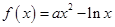 (
( 为常数).
为常数).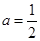 时,求
时,求 的单调递减区间;
的单调递减区间;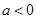 ,且对任意的
,且对任意的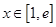 ,
,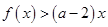 恒成立,求实数
恒成立,求实数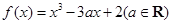 .
. 的单调递增区间;
的单调递增区间;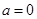 时,在曲线
时,在曲线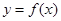 上是否存在两点
上是否存在两点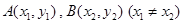 ,使得曲线在
,使得曲线在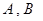 两点处的切线均与直线
两点处的切线均与直线 交于同一点?若存在,求出交点纵坐标的取值范围;若不存在,请说明理由;
交于同一点?若存在,求出交点纵坐标的取值范围;若不存在,请说明理由;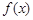 在区间
在区间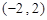 存在最大值
存在最大值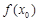 ,试构造一个函数
,试构造一个函数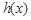 ,使得
,使得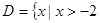 ,且
,且 ;②当
;②当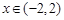 时,
时,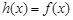 ;③在
;③在 中使
中使 值,从小到大组成等差数列.(只要写出函数
值,从小到大组成等差数列.(只要写出函数 ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为
 的值
的值 的三条不同切线,求
的三条不同切线,求 的取值范围
的取值范围 处的切线都过点(0,2),证明:当
处的切线都过点(0,2),证明:当 时,
时,
 的函数
的函数 是奇函数.
是奇函数.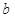 的值;
的值;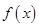 的单调性;
的单调性;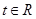 ,不等式
,不等式 恒成立,求
恒成立,求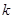 的取值范围.
的取值范围.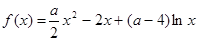 ,
, .
.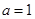 ,求函数
,求函数 的极值;
的极值;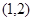 上有极值,求
上有极值,求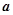 的取值范围.
的取值范围.