题目内容
(1)一次函数f(x)=kx+h(k≠0),若m<n有f(m)>0,f(n)>0,则对于任意x∈(m,n)都有f(x)>0,试证明之;(2)试用上面结论证明下面的命题:
若a,b,c∈R且|a|<1,|b|<1,|c|<1,则ab+bc+ca>-1.
答案:
解析:
解析:
| 证明:
(1)当k>0时,函数f(x)=kx+h在x∈R上是增函数,m<x<n,f(x)>f(m)>0; 当k<0时,函数f(x)=kx+h在x∈R上是减函数,m<x<n,f(x)>f(n)>0. 所以对于任意x∈(m,n)都有f(x)>0成立. (2)将ab+bc+ca+1写成(b+c)a+bc+1,构造函数f(x)=(b+c)x+bc+1.则 f(a)=(b+c)a+bc+1. 当b+c=0时,即b=-c, f(a)=bc+1=-c2+1. 因为|c|<1,所以f(a)=-c2+1>0. 当b+c≠0时,f(x)=(b+c)x+bc+1为x的一次函数. 因为|b|<1,|c|<1, f(1)=b+c+bc+1=(1+b)(1+c)>0, f(-1)=-b-c+bc+1=(1-b)(1-c)>0. 由问题(1)对于|a|<1的一切值f(a)>0,即 (b+c)a+bc+1=ab+ac+bc+1>0.
|

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
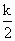 +f(x)成立.
+f(x)成立.