题目内容

已知集合M是满足下列性质的函数f(x)的全体：存在非零常数k，对任意x∈D(D为函数的定义域)，等式f(kx)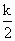＝＋f(x)成立．

(1)一次函数f(x)＝ax＋b(a≠0)是否属于集合M？说明理由；

(2)设函数f(x)＝logax(a＞1)的图像与y＝x的图像有公共点，试证明：f(x)＝logax∈M．

答案：
解析：

　　解　　(1)若一次函数f(x)∈M，即存在非零的常数k，使得等式akx＋b＝＋ax＋b，也就是a(k－1)x＝成立．显然对于任意x∈D＝R，a(k－1)x＝不能恒成立，故f(x)＝ax＋bM．

　　(2)如图，设函数f(x)＝logax(a＞1)的图像与函数y＝x的图像的公共点为B(t，t)，则显然t＞1．在x∈(1，t)上，函数f(x)＝logax(a＞1)有定义，故在函数f(x)＝logax(a＞1，x∈(1，t))的图像即弧AB上，必存在点C(k，)，使等式logax＝成立，其中1＜k＜t．

　　于是，f(kx)＝logakx＝logak＋logax＝＋logax＝＋f(x)，故f(x)＝logax∈M．


练习册系列答案
相关题目
已知集合M是满足下列性质的函数f（x）的全体：在定义域内存在x0，使得f（x0+1）=f（x0）+f（1）成立．
（1）函数f(x)=
1
x
是否属于集合M？说明理由；
（2）设函数f(x)=lg
a
x2+1
∈M，求a的取值范围；
（3）设函数y=2x图象与函数y=-x的图象有交点，证明：函数f（x）=2x+x2∈M．
已知集合M是满足下列性质的函数f（x）的全体：存在非零常数T，对任意x∈R，有f（x+T）=T•f（x）成立．
（1）函数f（x）=x是否属于集合M？说明理由；
（2）设函数f（x）=ax（a＞0，且a≠1）的图象与y=x的图象有公共点，证明：f（x）=ax∈M；
（3）若函数f（x）=sinkx∈M，求实数k的取值范围．
已知集合M是满足下列性质的函数f（x）的全体：存在非零常数k，对定义域中的任意x，等式f（kx）=
k2
+f（x）恒成立．
（1）判断一次函数f（x）=ax+b（a≠0）是否属于集合M；
（2）证明函数f（x）=log2x属于集合M，并找出一个常数k；
（3）已知函数f（x）=logax（ a＞1）与y=x的图象有公共点，证明f（x）=logax∈M．
已知集合M是满足下列条件的函数f（x）的全体；
①当x∈[0，+∞）时，函数值为非负实数；
②对于任意的s、t∈x[0，+∞），λ＞0，都有
f(x)+λf(t)
1+λ
≤f(
s+λt
1+λ
)
在三个函数f1（x）=x-1，f2(x)=2x-1，f3(x)=ln
x+1
中，属于集合M的是
f3（x）
f3（x）
（写出您认为正确的所有函数．）
（2011•嘉定区三模）已知集合M是满足下列两个条件的函数f（x）的全体：①f（x）在定义域上是单调函数；②在f（x）的定义域内存在闭区间[a，b]，使f（x）在[a，b]上的值域为[
a
2
 ， 
b
2
]．若函数g(x)=
x-1
+m，g（x）∈M，则实数m的取值范围是
(0 ， 
1
2
]
(0 ， 
1
2
]
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网