题目内容
已知平面向量
=(
,
),
=(sin
x,cos
x),函数f(x)=
•
.
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)将函数f(x)的图象上的所有的点向左平移1个单位长度,得到函数y=g(x)的图象,若函数y=g(x)+k在(-2,4)上有两个零点,求实数k的取值范围.
| a |
| 2 |
| 2 |
| b |
| π |
| 4 |
| π |
| 4 |
| a |
| b |
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)将函数f(x)的图象上的所有的点向左平移1个单位长度,得到函数y=g(x)的图象,若函数y=g(x)+k在(-2,4)上有两个零点,求实数k的取值范围.
分析:(I)利用数量积和两角和的正弦公式可得f(x),再利用周期公式即可得出周期T.
(II)依题意将函数f(x)的图象向左平移1个单位后得到函数y=g(x)=2sin[
(x+1)+
]=2cos
x,函数y=g(x)+k在(-2,4)上有两个零点,即函数y=g(x)与y=-k在x∈(-2,4)有两个交点,即可得出.
(II)依题意将函数f(x)的图象向左平移1个单位后得到函数y=g(x)=2sin[
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
解答:解:(Ⅰ)∵f(x)=
•
=
sin
x+
cos
x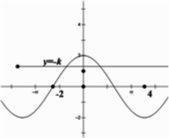
=2(
sin
x+
cos
x)
=2sin(
x+
),
∴T=
=8.
∴函数f(x)的最小正周期为8.
(Ⅱ)依题意将函数f(x)的图象向左平移1个单位后得到函数
y=g(x)=2sin[
(x+1)+
]=2cos
x,
函数y=g(x)+k在(-2,4)上有两个零点,即函数y=g(x)与y=-k在x∈(-2,4)有两个交点,如图所示.
∴当0<-k<2,即-2<k<0,
∴实数k取值范围为-2<k<0.
| a |
| b |
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |

=2(
| ||
| 2 |
| π |
| 4 |
| ||
| 2 |
| π |
| 4 |
=2sin(
| π |
| 4 |
| π |
| 4 |
∴T=
| 2π | ||
|
∴函数f(x)的最小正周期为8.
(Ⅱ)依题意将函数f(x)的图象向左平移1个单位后得到函数
y=g(x)=2sin[
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
函数y=g(x)+k在(-2,4)上有两个零点,即函数y=g(x)与y=-k在x∈(-2,4)有两个交点,如图所示.
∴当0<-k<2,即-2<k<0,
∴实数k取值范围为-2<k<0.
点评:本题考查了三角函数的图象与性质、数量积和两角和的正弦公式、数形结合等基础知识与基本技能方法,属于中档题.

练习册系列答案
相关题目
已知平面向量
=(2,4),
=(-2,2)若
=
+(
•
)
,则|
|等于( )
| a |
| b |
| c |
| a |
| a |
| b |
| b |
| c |
A、6
| ||
B、6
| ||
C、6
| ||
| D、6 |