题目内容
设函数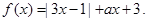
(Ⅰ)若 ,解不等式
,解不等式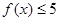 ;
;
(Ⅱ)若函数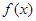 有最小值,求实数
有最小值,求实数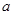 的取值范围.
的取值范围.
(Ⅰ)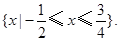 (Ⅱ)
(Ⅱ)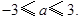
解析试题分析:(Ⅰ)分类去掉绝对值符号,化为整式不等式再解,最后取并集即可.
(Ⅱ)把函数f(x)化为分段函数,然后再找出f(x)有最小值的充要条件解之即可.
试题解析:(Ⅰ)a=1时,f(x)=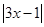 +x+3
+x+3
当x≥ 时,f(x)≤5可化为3x-1+x+3≤5,解得
时,f(x)≤5可化为3x-1+x+3≤5,解得 ≤x
≤x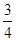 ;
;
当x< 时,f(x)≤5可化为-3x+1+x+3≤5,解得-
时,f(x)≤5可化为-3x+1+x+3≤5,解得-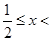
 ,
,
综上可得,原不等式的解集为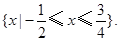
(Ⅱ)f(x)= 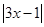 +x+3=
+x+3=
函数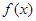 有最小值的充要条件是
有最小值的充要条件是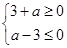 ,解得
,解得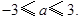
考点:1.绝对值不等式;2.分段函数及其求函数值.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
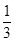 ,|2x-y|<
,|2x-y|<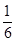 ,求证:|y|<
,求证:|y|<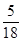 .
.
 的解集;
的解集;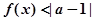 的解集非空,求实数
的解集非空,求实数 的取值范围.
的取值范围.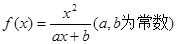 ,且方程
,且方程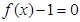 有两个实根为
有两个实根为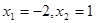 .
. 的解析式 ;
的解析式 ;  ,解关于x的不等式:
,解关于x的不等式: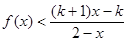 .
.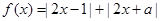 ,
,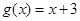 .
. 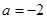 时,求不等式
时,求不等式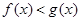 的解集;
的解集;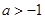 ,且当
,且当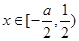 时,
时,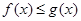 ,求
,求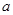 的取值范围。
的取值范围。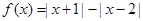 .
.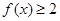 ;
;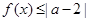 的解集为
的解集为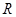 ,求实数
,求实数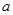 的取值范围.
的取值范围.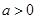 ,
,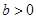 ,
, .求证:
.求证: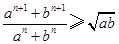 .
.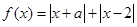
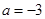 时,求不等式
时,求不等式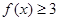 的解集;
的解集;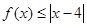 在
在 上恒成立,求
上恒成立,求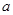 的取值范围。
的取值范围。