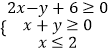题目内容
【题目】若函数y=ksin（kx+φ）（ 
）与函数y=kx﹣k2+6的部分图象如图所示，则函数f（x）=sin（kx﹣φ）+cos（kx﹣φ）图象的一条对称轴的方程可以为（ ） 
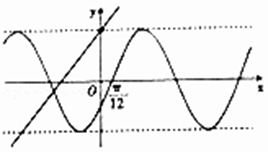
A.
B.
C.
D.
【答案】B
【解析】解：若函数y=ksin（kx+φ）（ 
）与函数y=kx﹣k2+6的部分图象如图所示，
根据函数y=ksin（kπ+φ）（k＞0，|φ|＜ 
）的最大值为k，∴﹣k2+6=k，∴k=2．
把点（ 
，0）代入y=2sin（2x+φ）可得 sin（ 
+φ）=0，∴φ=﹣ ，∴入y=2sin（2x﹣ ）．
则函数f（x）=sin（kx﹣φ）+cos（kx﹣φ）=2sin（2x+ ）+2cos（2x+ ）= 
sin（2x+ + 
）= sin（2x+ 
）．
令2x+ =kπ+ ，求得x= 
+ 
，k∈Z，故f（x）的图象的对称轴的方程为得x= + ，k∈Z
当k=1时，可得函数f（x）=sin（kx﹣φ）+cos（kx﹣φ）图象的一条对称轴的方程可以为 
，
故选：B．
由函数的最大值求出A，由特殊点的坐标求出φ的值，可得函数的解析式，再利用三角恒等变换化简f（x）的解析式，再利用正弦函数的图象的对称性求得f（x）的图象的一条对称轴的方程．
练习册系列答案
阅读快车系列答案
相关题目
