题目内容
1.已知点(a,b)与点(2,0)位于直线2x+3y-1=0的同侧,且a>0,b>0,则z=$\frac{4b+1}{4a-1}$的取值范围是( )| A. | (-$\frac{7}{3}$,1) | B. | ($-∞,-\frac{7}{3}$)∪(1,+∞) | C. | ($-∞,-\frac{7}{3}$)∪(0,+∞) | D. | ($-\frac{7}{3}$,0) |
分析 根据题意求出2a+3b-1>0,画出不等式组$\left\{\begin{array}{l}{2a+3b-1>0}\\{a>0}\\{b>0}\end{array}\right.$表示的平面区域,再化简z,
根据图形,利用直线的斜率求出z的取值范围.
解答 解:∵点(a,b)和(2,0)在直线2x+3y-1=0的同侧,
∴(2a+3b-1)(4+0-1)>0,
即2a+3b-1>0;
又a>0,且b>0,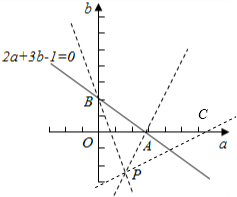
∴$\left\{\begin{array}{l}{2a+3b-1>0}\\{a>0}\\{b>0}\end{array}\right.$;
且z=$\frac{4b+1}{4a-1}$=$\frac{b-(-\frac{1}{4})}{a-\frac{1}{4}}$,.
画出不等式组表示的平面区域,
设P($\frac{1}{4}$,-$\frac{1}{4}$),A($\frac{1}{2}$,0),B(0,$\frac{1}{3}$),如图所示;
计算kPB=$\frac{\frac{1}{3}+\frac{1}{4}}{0-\frac{1}{4}}$=-$\frac{7}{3}$,
∴z<-$\frac{7}{3}$,
又根据图形得,z>0,
∴z∈(-∞,-$\frac{7}{3}$)∪(0,+∞).
故选:C.
点评 本题考查了不等式组表示平面区域的应用问题,也考查了直线斜率的应用问题,是综合性题目.

练习册系列答案
相关题目
10.若抛物线y=$\frac{1}{2}$x2上距点A(0,a)(a>0)最近的点恰好是顶点,则a的取值范围是( )
| A. | a>0 | B. | 0<a≤1 | C. | 0<a≤$\frac{1}{2}$ | D. | a≥1 |