题目内容
6．已知某三角形的面积为S，证明：用斜二测画法得到的其直观图的面积为S′=$\frac{\sqrt{2}}{4}$S．分析 根据斜二测画法与平面直观图的关系进行求解即可．
解答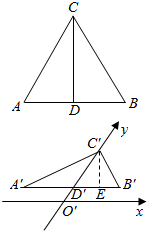 
证明：如图△A'B'C'是△ABC的直观图，则A'B'=AB，C'D'为△ABC的高CD的一半，
高C'E=C'D'sin45°=$\frac{\sqrt{2}}{4}$CD，
∴三角形△A'B'C'的面积为S′$\frac{1}{2}×A′B′×\frac{\sqrt{2}}{4}CD$=$\frac{\sqrt{2}}{4}$S．
点评 本题主要考查斜二测画法的应用，要求熟练掌握斜二测对应边长的对应关系，比较基础．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f（x）=|x|（x-2）．
1．已知点（a，b）与点（2，0）位于直线2x+3y-1=0的同侧，且a＞0，b＞0，则z=$\frac{4b+1}{4a-1}$的取值范围是（ ）
| A． | （-$\frac{7}{3}$，1） | B． | （$-∞，-\frac{7}{3}$）∪（1，+∞） | C． | （$-∞，-\frac{7}{3}$）∪（0，+∞） | D． | （$-\frac{7}{3}$，0） |
