题目内容
【题目】已知数列{an}的前n项和为Sn(n∈N*),且满足an+2Sn=2n+2.
(1)求数列{an}的通项公式;
(2)求证: ![]() .
.
【答案】
(1)解:∵an+2Sn=2n+2,令n=1,得 ![]() .
.
由an+2Sn=2n+2得 n≥2时,an﹣1+2Sn﹣1=2(n﹣1)+2,
两式相减得;3an=an﹣1+2,
∴ ![]() ,
,
∴数列{an﹣1}是以首项为 ![]() ,公比为
,公比为 ![]() 的等比数列,
的等比数列,
∴ ![]() ,∴
,∴ ![]() .
.
(2)证明:
∵ 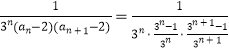 =
= ![]() ,
,
∴ ![]()
= ![]() =
= ![]() =
= ![]()
【解析】(1)由an+2Sn=2n+2,利用递推关系可得:3an=an﹣1+2,变形为 ![]() ,再利用等比数列的通项公式即可得出.(2)利用“裂项求和”方法与数列的单调性即可得出.
,再利用等比数列的通项公式即可得出.(2)利用“裂项求和”方法与数列的单调性即可得出.
【考点精析】本题主要考查了数列的通项公式的相关知识点,需要掌握如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.

练习册系列答案
相关题目
【题目】学校某文具商店经营某种文具,商店每销售一件该文具可获利3元,若供大于求则削价处理,每处理一件文具亏损1元;若供不应求,则可以从外部调剂供应,此时每件文具仅获利2元.为了了解市场需求的情况,经销商统计了去年一年(52周)的销售情况.
销售量(件) | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
周数 | 2 | 4 | 8 | 13 | 13 | 8 | 4 |
以去年每周的销售量的频率为今年每周市场需求量的概率.
(1)要使进货量不超过市场需求量的概率大于0.5,问进货量的最大值是多少?
(2)如果今年的周进货量为14,写出周利润Y的分布列;
(3)如果以周利润的期望值为考虑问题的依据,今年的周进货量定为多少合适?

