题目内容
设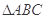 的内角
的内角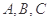 所对边的长分别是
所对边的长分别是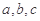 ,且
,且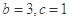 ,
,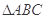 的面积为
的面积为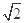 ,求
,求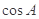 与
与 的值.
的值.
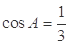 ,
,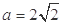 ;或
;或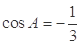 ,
,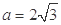 .
.
解析试题分析:
解题思路:先利用三角形的面积公式求出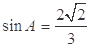 ,因为无法判定角A 的范围,因此利用同角三角函数基本关系式求出
,因为无法判定角A 的范围,因此利用同角三角函数基本关系式求出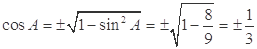 ,再利用余弦定理分类讨论求边a..
,再利用余弦定理分类讨论求边a..
规律总结:解三角形问题,主要涉及三角关系、三边关系、边角关系和面积;所用知识主要有正弦定理、余弦定理、三角形的面积公式等,但要注意解的个数问题.
试题解析:由三角形面积公式,得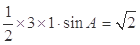 ,故
,故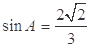 .
.
∵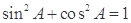 ,∴
,∴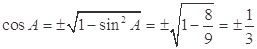 ;
;
当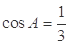 时,由余弦定理得
时,由余弦定理得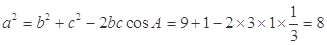 ,
,
所以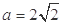 ;
;
当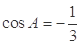 时,由余弦定理得,
时,由余弦定理得,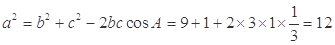 ,
,
所以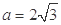 .
.
考点:1.解三角形;2.三角函数基本关系式.

练习册系列答案
相关题目
 sinA –cos(B+C)的取值范围.
sinA –cos(B+C)的取值范围. 点D、E分别为AC、BC边的中点,且BD=
点D、E分别为AC、BC边的中点,且BD= ,
,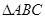 的内角
的内角 所对边的长分别是
所对边的长分别是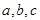 ,且
,且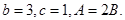
 的值; (Ⅱ)求
的值; (Ⅱ)求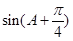 的值.
的值.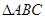 中,
中,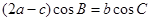
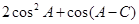 的取值范围.
的取值范围.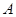 ,
,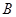 ,
, 是的内角,
是的内角, ,
, ,
, 分别是其对边长,向量,,.
分别是其对边长,向量,,. 、b、c ,若(
、b、c ,若( b – c)cosA=acosC,则cosA=______
b – c)cosA=acosC,则cosA=______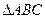 中,
中, 、
、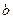 、
、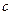 分别是角A、B、C所对的边,
分别是角A、B、C所对的边,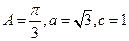 ,
, 中,
中, ,则
,则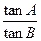 = 。
= 。