题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c且满足c sinA="a" cosC.
(1)求角C的大小;
(2)求 sinA –cos(B+C)的取值范围.
sinA –cos(B+C)的取值范围.
(1)C= ;(2)
;(2)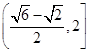
解析试题分析:(1)由正弦定理得sinCsinA="sinAcosC" , 所以tanC=1,则C=
(2) sinA –cos(B+C)=
sinA –cos(B+C)=  sinA –cos(
sinA –cos(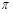 -A )
-A )
= sinA –cosA=2sin(A+
sinA –cosA=2sin(A+ )
)
又 0 < A< 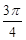 ,
,  < A+
< A+ <
< 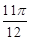 ,
,
所以 sinA –cos(B+C) 的取值范围
sinA –cos(B+C) 的取值范围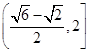
试题解析:(1)已知c sinA="a" cosC
由正弦定理得sinCsinA="sinAcosC" ,
因为0<A<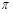 , 所以sinA>0, 得sinC="cosC" ,
, 所以sinA>0, 得sinC="cosC" ,
又cosC ≠0,所以tanC=1,则C=
(2)已知A+B+C=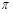 ,所以
,所以 sinA –cos(B+C)=
sinA –cos(B+C)=  sinA –cos(
sinA –cos(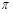 -A ) =
-A ) = sinA –cosA=2sin(A+
sinA –cosA=2sin(A+ )
)
又C= ,所以0 < A<
,所以0 < A< 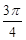 ,
,  < A+
< A+ <
< 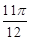 ,
,
所以sin(A+ )
)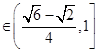 ,
,
所以2sin(A+ )
)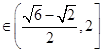
综上所述, sinA –cos(B+C) 的取值范围
sinA –cos(B+C) 的取值范围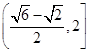
考点:正弦定理,三角函数恒等变换.

练习册系列答案
相关题目
 的内角
的内角 所对的边为
所对的边为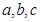 ;则下列命题正确的是
;则下列命题正确的是
 ;则
;则
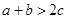 ;则
;则 ;则
;则
 ;则
;则
 ;则
;则
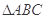 的内角
的内角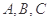 所对边的长分别是
所对边的长分别是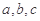 ,且
,且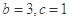 ,
,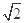 ,求
,求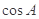 与
与 的值.
的值. 中,角
中,角 所对的边分别是
所对的边分别是 ,已知
,已知 .
. ,求
,求 ;
; ,
, ,求
,求 .
. ,求△ABC的周长L的取值范围.
,求△ABC的周长L的取值范围. .
.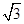 ,c=5,求b.
,c=5,求b. ,
, ,
, .若
.若 ,则BD=___ __
,则BD=___ __ 中,
中, 分别为
分别为 的对边.如果
的对边.如果 ,
, ,那么
,那么 ___▲___.
___▲___. 距离为10海里的C处,此时得知,该渔船沿北偏东
距离为10海里的C处,此时得知,该渔船沿北偏东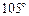 方向,以每小时9海里的速度向一小岛靠近,舰艇时速21海里,则舰艇到达渔船的最短时间是___________.
方向,以每小时9海里的速度向一小岛靠近,舰艇时速21海里,则舰艇到达渔船的最短时间是___________.