题目内容
选修
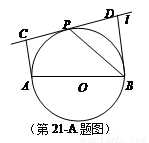
4-1:几何证明选讲如下图,已知△
ABC中的两条角平分线AD和CE相交于H,∠B=60°,F在AC上,且AE=AF.
(Ⅰ)证明:B,D,H,E四点共圆:
(Ⅱ)证明:CE平分∠DEF.
答案:
解析:
解析:
|
解: (Ⅰ)在△ABC中,因为∠B=60°,所以∠ BAC+∠BCA=120°.因为 AD,CE是角平分线,所以∠ HAC+∠HCA=60°,故∠ AHC=120°.于是∠ EHD=∠AHC=120°.因为∠ EBD+∠EHD=180°,所以 B,D,H,E四点共圆.(Ⅱ)连结BH,则BH为∠ABC的平分线,得∠HBD=30°
由 (Ⅰ)知B,D,H,E四点共圆,所以∠ CED=∠HBD=30°.又∠ AHE=∠EBD=60°,由已知可得EF⊥AD,可得∠ CEF=30°.所以 CE平分∠DEF. |

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
A.选修4-1:几何证明选讲
|
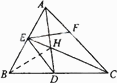
如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD.求证:(1)l是⊙O的切线;(2)PB平分∠ABD.
B.选修4-2:矩阵与变换
(本小题满分10分)
已知点A在变换:T:→=作用后,再绕原点逆时针旋转90°,得到点B.若点B坐标为(-3,4),求点A的坐标.
C.选修4-4:坐标系与参数方程
(本小题满分10分)
求曲线C1:被直线l:y=x-所截得的线段长.
D.选修4-5:不等式选讲
(本小题满分10分)
已知a、b、c是正实数,求证:≥.
 (2013•太原一模)选修4一1:几何证明选讲
(2013•太原一模)选修4一1:几何证明选讲
 选修4一1:几何证明选讲
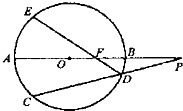
选修4一1:几何证明选讲 为半圆
为半圆 的直径,
的直径, ,
, 为半圆上一点,过点
为半圆上一点,过点 ,过点
,过点 作
作 于
于 ,交半圆于点
,交半圆于点 ,
, .
.
 平分
平分 ;
; 的长.
的长. ABC中的两条角平分线
ABC中的两条角平分线 和
和 相交于
相交于 ,
, B=60
B=60 ,
, 在
在 上,且
上,且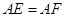 。
。  四点共圆;
四点共圆;