题目内容
 (2013•太原一模)选修4一1:几何证明选讲
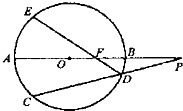
(2013•太原一模)选修4一1:几何证明选讲如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P.E为⊙O上一点,
 |
| AC |
 |
| AE |
(I)证明:DF•EF=OF•FP;
(II)当AB=2BP时,证明:OF=BF.
分析:(I)利用弧长相等,转化为角相等,通过三角形相似证明:DF•EF=OF•FP;
(II)设BP=a,ly AB=2BP,通过相交弦定理以及数量关系的转化证明:OF=BF.
(II)设BP=a,ly AB=2BP,通过相交弦定理以及数量关系的转化证明:OF=BF.
解答:.(I)证明:因为
=
,∴∠AOE=∠CDE,∴∠EOF=∠PDF,
又∠EFO=∠PFD,
∴△OFE∽△PFD,∴
=
,
∴DF•EF=OF•FP;
(II)设BP=a,由AB=2BP,得AO=BO=BP=a,
由相交弦定理得:DF•EF=AF•BF,
∴AF•BF=OF•FP,
∴OF•(a+BF)=(a+OF)•BF,∴OF=BF.
 |
| AC |
 |
| AE |
又∠EFO=∠PFD,
∴△OFE∽△PFD,∴
| OF |
| DF |
| EF |
| PF |
∴DF•EF=OF•FP;
(II)设BP=a,由AB=2BP,得AO=BO=BP=a,
由相交弦定理得:DF•EF=AF•BF,
∴AF•BF=OF•FP,
∴OF•(a+BF)=(a+OF)•BF,∴OF=BF.
点评:本题考查直线与圆的关系,三角形相似以及相交弦定理的应用,考查计算能力与转化思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目