题目内容
 选修4一1:几何证明选讲
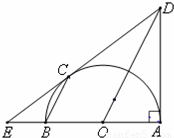
选修4一1:几何证明选讲如图,C是以AB为直径的半圆O上的一点,过C的直线交直线AB于E,交过A点的切线于D,BC∥OD.
(Ⅰ)求证:DE是圆O的切线;
(Ⅱ)如果AD=AB=2,求EB.
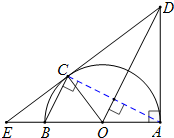
分析:(Ⅰ)要证DE是圆O的切线,连接AC,只需证出∠DAO=90°,由BC∥OD⇒OD⊥AC,则OD是AC的中垂线.通过△AOC,△BOC均为等腰三角形,即可证得∠DAO=90°.
(Ⅱ)由 BC∥OD⇒∠CBA=∠DOA,结合∠BCA=∠DAO,得出△ABC∽△AOD,利用比例线段求出EB.
(Ⅱ)由 BC∥OD⇒∠CBA=∠DOA,结合∠BCA=∠DAO,得出△ABC∽△AOD,利用比例线段求出EB.
解答:(Ⅰ)证:连接AC,AB是直径,则BC⊥AC
由BC∥OD⇒OD⊥AC
则OD是AC的中垂线⇒∠OCA=∠OAC,∠DCA=∠DAC,
⇒∠OCD=∠OCA+∠DCA=∠OAC+∠DAC=∠DAO=90°.
⇒OC⊥DE,所以DE是圆O的切线.
(Ⅱ) BC∥OD⇒∠CBA=∠DOA,∠BCA=∠DAO⇒△ABC∽△AOD
⇒
=
⇒BC=
=
=
⇒
=
⇒
=
⇒
=
⇒BE=
由BC∥OD⇒OD⊥AC

则OD是AC的中垂线⇒∠OCA=∠OAC,∠DCA=∠DAC,
⇒∠OCD=∠OCA+∠DCA=∠OAC+∠DAC=∠DAO=90°.
⇒OC⊥DE,所以DE是圆O的切线.
(Ⅱ) BC∥OD⇒∠CBA=∠DOA,∠BCA=∠DAO⇒△ABC∽△AOD
⇒
| BC |
| OA |
| AB |
| OD |
| OA•AB |
| OD |
| 1×2 | ||
|
2
| ||
| 5 |
| BC |
| OD |
| 2 |
| 5 |
| BE |
| OE |
| 2 |
| 5 |
| BE |
| OB |
| 2 |
| 3 |
⇒BE=
| 2 |
| 3 |
点评:本题考查圆的切线的证明,与圆有关的比例线段.准确掌握与圆有关的线、角的性质是解决此类问题的基础和关键.

练习册系列答案
相关题目
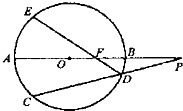 (2013•太原一模)选修4一1:几何证明选讲
(2013•太原一模)选修4一1:几何证明选讲
 ,DE交AB于点F.
,DE交AB于点F.