题目内容
【题目】已知函数f(x)=|x﹣2|+|2x+1|.
(Ⅰ)解不等式f(x)>5;
(Ⅱ)若关于x的方程 ![]() =a的解集为空集,求实数a的取值范围.
=a的解集为空集,求实数a的取值范围.
【答案】解:(Ⅰ)解不等式|x﹣2|+|2x+1|>5, x≥2时,x﹣2+2x+1>5,解得:x>2;
﹣ ![]() <x<2时,2﹣x+2x+1>5,无解,
<x<2时,2﹣x+2x+1>5,无解,
x≤﹣ ![]() 时,2﹣x﹣2x﹣1>5,解得:x<﹣
时,2﹣x﹣2x﹣1>5,解得:x<﹣ ![]() ,
,
故不等式的解集是(﹣∞,﹣ ![]() )∪(2,+∞);
)∪(2,+∞);
(Ⅱ)f(x)=|x﹣2|+|2x+1|= 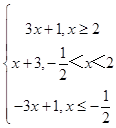 ,
,
故f(x)的最小值是 ![]() ,所以函数f(x)的值域为[
,所以函数f(x)的值域为[ ![]() ,+∞),
,+∞),
从而f(x)﹣4的取值范围是[﹣ ![]() ,+∞),
,+∞),
进而 ![]() 的取值范围是(﹣∞,﹣
的取值范围是(﹣∞,﹣ ![]() ]∪(0,+∞).
]∪(0,+∞).
根据已知关于x的方程 ![]() =a的解集为空集,所以实数a的取值范围是(﹣
=a的解集为空集,所以实数a的取值范围是(﹣ ![]() ,0].
,0].
【解析】(Ⅰ)分类讨论求得原不等式解集.(Ⅱ)由分段函数f(x)的解析式可得f(x)的单调性,由此求得函数f(x)的值域,求出 ![]() 的取值范围.再根据关于x的方程
的取值范围.再根据关于x的方程 ![]() =a的解集为空集,求得实数a的取值范围.
=a的解集为空集,求得实数a的取值范围.
【考点精析】本题主要考查了绝对值不等式的解法的相关知识点,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
优秀 | 非优秀 | 总计 | |
甲班 | 10 | ||
乙班 | 30 | ||
总计 | 105 |
已知在全部105人中随机抽取1人为优秀的概率为![]() .
.
(1)请完成上面的列联表;
(2)根据列联表的数据,若按95%的可靠性要求,能否认为“成绩与班级有关系”?
参考公式:K2=![]()
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |