Question

【题目】定义：圆心到直线的距离与圆的半径之比为直线关于圆的距离比.

（1）设圆求过（2,0）的直线关于圆的距离比的直线方程；

（2）若圆与轴相切于点（0,3）且直线= 关于圆的距离比，求此圆的的方程；

（3）是否存在点，使过的任意两条互相垂直的直线分别关于相应两圆的距离比始终相等？若存在，求出相应的点点坐标；若不存在，请说明理由.

Answer 1

【答案】（1）；（2）或 ；（3）存在.

【解析】试题分析：（1）设过的直线方程为，求得已知圆的圆心和半径，由新定义，可得方程，求得，即可得到所求直线方程；（2）设圆的方程为，由题意可得，解方程可得， ， ，进而得到所求圆的方程；（3）假设存在点，设过的两直线为和，求得两圆的圆心和半径，由新定义可得方程，化简整理可得或，再由恒成立思想可得， 的方程，解方程可得的坐标．

试题解析：（1）设过的直线方程为
∵圆的圆心为，半径为
∴根据题意可得
∴，即所求直线为;
（2）设圆的方程为
根据题意可得
∴解方程可得或，则有圆的方程为或
（3）假设存在点，设过的两直线为和

又∵的圆心为，半径为， 的圆心为，半径为
∴根据题意可得，即或
∴或,
∴或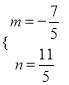，则存在这样的点和，使得使过的任意两条互相垂直的直线分别关于相应两圆的距离比始终相等.