题目内容
8.正方形AC1中,点P是DD1中点,点O是底面中心,求证:B1O⊥平面PAC.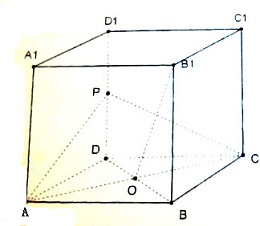
分析 首先在矩形BB1D1D中,利用直角三角形的正切定义得到∠POD=∠BB1O,从而证出PO⊥B1O,然后利用直线AC与平面BB1D1D证出AC⊥B1O,最后用直线与平面垂直的判定定理,可得到B1O⊥平面PAC.
解答 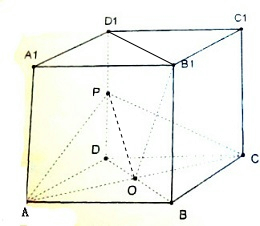 证明:设正方体边长为1,连接B1D1,连接PO,在矩形BB1D1D中,BD=$\sqrt{2}$,OD=OB=$\frac{\sqrt{2}}{2}$,
证明:设正方体边长为1,连接B1D1,连接PO,在矩形BB1D1D中,BD=$\sqrt{2}$,OD=OB=$\frac{\sqrt{2}}{2}$,
∴Rt△PDO中,PD=$\frac{1}{2}$,
∴tan∠POD=$\frac{PD}{OD}$=$\frac{\sqrt{2}}{2}$同理,Rt△BOB1中,tan∠BB1O=$\frac{OB}{B{B}_{1}}$=$\frac{\sqrt{2}}{2}$,
∴锐角∠POD=∠BB1O=90°-∠B1OB⇒∠POD+∠B1OB=90°,
∴∠POB1=90°⇒PO⊥B1O,
∵BB1⊥平面ABCD,AC?平面ABCD,
∴AC⊥BB1,
∵AC⊥BD,BD∩BB1=B,
∴AC⊥平面BB1D1D,结合B1O?平面BB1D1D,
∴AC⊥B1O,
∵PO∩AC=O,
∴B1O⊥平面ACP.
点评 本题主要考查空间直线与平面的位置关系等基础知识,考查空间想象能力,推理论证能力和转化与化归的思想,属于中档题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
19.复数$\frac{2}{i-1}$的共轭复数是( )
| A. | i+1 | B. | i-1 | C. | -1-i | D. | 1-i |
 如图,在△ABC和△AEF中,B是EF的中点,AB=EF=1,CA=CB=2,若$\overrightarrow{AB}$•$\overrightarrow{AE}$+
如图,在△ABC和△AEF中,B是EF的中点,AB=EF=1,CA=CB=2,若$\overrightarrow{AB}$•$\overrightarrow{AE}$+ 如图,已知△OCB中,B、C关于点A对称,D是将OB分成2:1的一个内分点,DC和OA交于点E,设$\overrightarrow{OA}=\overrightarrow a,\overrightarrow{OB}=\overrightarrow b$.
如图,已知△OCB中,B、C关于点A对称,D是将OB分成2:1的一个内分点,DC和OA交于点E,设$\overrightarrow{OA}=\overrightarrow a,\overrightarrow{OB}=\overrightarrow b$.