题目内容
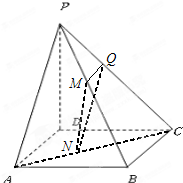如图，四棱锥P-ABCD中，底面ABCD是正方形，PD=AB，PD⊥底面ABCD，M，N，Q分别在PB，AC，PC上，且| PM |
| MB |
| AN |
| NC |
| PQ |
| QC |
（1）求证：平面MNQ∥平面PAD．
（2）求直线PB与平面面MNQ所成角的正弦值．
分析：（1）要证平面MNQ∥平面PAD，可由
=
⇒MQ∥BC⇒MQ∥平面PAD．同理NQ∥平面PAD证出．
（2）由（1），直线PB与平面面MNQ所成角等于直线PB与平面PAD所成角．证出BA⊥平面PAD，∠BPA为直线PB与平面MNQ所成角，
| PM |
| MB |
| PQ |
| QC |
（2）由（1），直线PB与平面面MNQ所成角等于直线PB与平面PAD所成角．证出BA⊥平面PAD，∠BPA为直线PB与平面MNQ所成角，
解答：（1）证明：
=
⇒MQ∥BC，∵BC∥AD，∴MQ∥AD，
MQ?平面PAD，AD?平面PAD，∴MQ∥平面PAD．
同理
=
⇒NQ∥AP，NQ?平面PAD，AP?平面PAD，∴NQ∥平面PAD．
MQ，NQ?平面MNQ，MQ∩NQ=Q，
∴平面MNQ∥平面PAD．
（2）解：由（1），直线PB与平面面MNQ所成角等于直线PB与平面PAD所成角．
⇒∠BPA为直线PB与平面PAD所成角，
设正方形ABCD边长为1，则PD=AB=1，直角三角形△PDA斜边PA=
，直角三角形△BPA斜边PB=
，
sin∠BPA=
=
=
．
| PM |
| MB |
| PQ |
| QC |
MQ?平面PAD，AD?平面PAD，∴MQ∥平面PAD．
同理
| AN |
| NC |
| PQ |
| QC |
MQ，NQ?平面MNQ，MQ∩NQ=Q，
∴平面MNQ∥平面PAD．
（2）解：由（1），直线PB与平面面MNQ所成角等于直线PB与平面PAD所成角．
|
|
设正方形ABCD边长为1，则PD=AB=1，直角三角形△PDA斜边PA=
| 2 |
| 3 |
sin∠BPA=
| AB |
| PB |
| 1 | ||
|
| ||
| 3 |
点评：本题考查空间直线、平面位置关系的判断，线面角大小求解，考查空间想象能力、推理论证、计算、转化能力．
练习册系列答案
相关题目
如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，
如图，四棱锥P-ABCD中，底面ABCD是直角梯形，AB∥CD，∠DAB=60°，AB=AD=2CD=2，侧面PAD⊥底面ABCD，且△PAD为等腰直角三角形，∠APD=90°，M为AP的中点．
如图，四棱锥P-ABCD的底面ABCD是矩形，AB=2，
如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥底面ABCD，且PA=AB=1，
如图，四棱锥P-ABCD，PA⊥平面ABCD，ABCD是直角梯形，DA⊥AB，CB⊥AB，PA=2AD=BC=2，AB=