Question

（2012•深圳二模）设函数f（x）=x²+bx+c，其中b，c是某范围内的随机数，分别在下列条件下，求事件A“f（1）≤5且f（0）≤3”发生的概率．
（1）若随机数b，c∈{1，2，3，4}；
（2）已知随机函数Rand（　　）产生的随机数的范围为{x|0≤x≤1}，b，c是算法语句b=4*Rand（　　）和c=4*Rand（　　）的执行结果．（注：符号“*”表示“乘号”）

Answer 1

分析：（1）由f（x）=x²+bx+c知，事件A“f（1）≤5且f（0）≤3”，即

b+c≤4 c≤3

，随机数b，c∈{1，2，3，4}，共等可能地产生16个数对，事件A：

b+c≤4 c≤3

包含了其中6个数对，从而可求事件A发生的概率；
（2）由题意，b，c均是区间[0，4]中的随机数，产生的点（b，c）均匀地分布在边长为4的正方形区域Ω中，事件A：

b+c≤4 c≤3

所对应的区域为的梯形，从而可求事件A的发生概率．

解答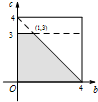：解：（1）由f（x）=x²+bx+c知，事件A“f（1）≤5且f（0）≤3”，即

b+c≤4 c≤3

（1分）
因为随机数b，c∈{1，2，3，4}，所以共等可能地产生16个数对（b，c），
列举如下：（1，1），（1，2），（1，3），（1，4），（2，1），（2，2），（2，3），（2，4），（3，1），（3，2），（3，3），（3，4），（4，1），（4，2），（4，3），（4，4），（4分）
事件A：

b+c≤4 c≤3

包含了其中6个数对（b，c），即：（1，1），（1，2），（1，3），（2，1），（2，2），（3，1），（6分）
所以P(A)=

6

16

=

3

8

，即事件A发生的概率为

3

8

 （7分）
（2）由题意，b，c均是区间[0，4]中的随机数，产生的点（b，c）均匀地分布在边长为4的正方形区域Ω中（如图），其面积S（Ω）=16．（8分）
事件A：

b+c≤4 c≤3

所对应的区域为如图所示的梯形（阴影部分），
其面积为：S（A）=

1

2

×(1+4)×3=

15

2

．（10分）
所以P(A)=

S(A)

S(Ω)

=

15 2

16

=

15

32

，即事件A的发生概率为

15

32

．（12分）

点评：本题主要考查随机数、随机函数的定义，古典概型，几何概型，线性规划等基础知识，考查学生转换问题的能力，数据处理能力．